Biểu đồ dưới đây biểu diễn tỉ lệ phần trăm khối lượng gạo bán được của các loại gạo trong một ngày của cửa hàng A:
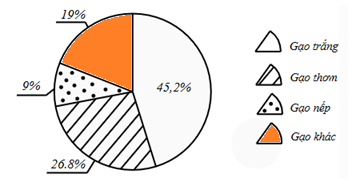
Biết rằng ngày hôm đó cửa hàng A bán được 18 kg gạo nếp. Hỏi cửa hàng bán được bao nhiêu kg gạo trắng trong ngày hôm đó?
Biểu đồ dưới đây biểu diễn tỉ lệ phần trăm khối lượng gạo bán được của các loại gạo trong một ngày của cửa hàng A:
Biết rằng ngày hôm đó cửa hàng A bán được 18 kg gạo nếp. Hỏi cửa hàng bán được bao nhiêu kg gạo trắng trong ngày hôm đó?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án: 90,4
Theo biểu đồ ta có: Cửa hàng bán được \(9\% \) khối lượng gạo nếp, \(45,2\% \) gạo trắng ngày hôm đó.
Hôm đó cửa hàng bán được số kg gạo là:\(18:9\% = 200\;\left( {{\rm{kg}}} \right).\)
Hôm đó cửa hàng bán được số kg gạo trắng là: \(200 \cdot 45,2\% = 90,4\;\left( {{\rm{kg}}} \right).\)
Vậy cửa hàng hôm đó bán được 90,4 kg gạo trắng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: a) Đúng. b) Sai. c) Sai. d) Đúng.
a) Các kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số lẻ”, đó là: \(1;\,\,3;\,\,5;....;\,\,37;\,\,39.\)
Do đó, có \(20\) kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số lẻ”.
Do đó, ý a) là đúng.
b) Các kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút là bình phương của một số” là:
\(1;\,\,4;\,\,9;\,\,16;\,\,25;\,\,36\).
Do đó, có 6 kết quả thuận lợi cho biến cố này.
Do đó, ý b) là sai.
c) Xác suất của biến cố “Số xuất hiện trên thẻ được rút là bình phương của một số” là: \(\frac{6}{{40}} = \frac{3}{{20}}.\)
Do đó, ý c) là sai.
d) Kết quả thuận lợi của biến cố: “Số xuất hiện trên thẻ được rút ra là lập phương của một số” là: \(1;\,\,8;\,\,27.\)
Do đó có 3 kết quả thuận lợi cho biến cố này.
Vậy xác suất của biến cố này là \(\frac{3}{{40}} = 0,075.\)
Do đó, ý d) là đúng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Đáp án: 0,4
Các kết quả có thể xảy ra khi lập một số có ba chữ số khác nhau từ các số \(1,2,3,4,6\) là: \(5.4.3 = 60\).
Gọi \(A\) là biến cố “Số được chọn chia hết cho 3”.
Nhận thấy ta lập được 4 bộ số gồm 3 chữ số có tổng chia hết cho 3 là:
\(\left( {1;2;3} \right);{\rm{ }}\left( {1;2;6} \right);{\rm{ }}\left( {2;3;4} \right);{\rm{ }}\left( {2;4;6} \right)\).
Mỗi bộ số, ta lập được các số có ba chữ số là: \(3.2.1 = 6\) (số)
Do đó, 4 bộ số thì lập được các số có tổng chữ số chia hết cho 3 là: \(6.4 = 24\) (số)
Suy ra số kết quả thuận lợi của biến cố “Số được chọn chia hết cho 3” là: \(24\)số.
Xác suất của biến cố \(A\) là: \(\frac{{24}}{{60}} = \frac{2}{5} = 0,4.\)
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập