Cho \(\Delta ABC\) có chu vi bằng \(40\;{\rm{cm}}{\rm{.}}\) Gọi \(M,\;N\) lần lượt là trung điểm của \(AB,\;AC.\) Chu vi \(\Delta AMN\) bằng bao nhiêu \({\rm{cm}}?\)
Cho \(\Delta ABC\) có chu vi bằng \(40\;{\rm{cm}}{\rm{.}}\) Gọi \(M,\;N\) lần lượt là trung điểm của \(AB,\;AC.\) Chu vi \(\Delta AMN\) bằng bao nhiêu \({\rm{cm}}?\)
Quảng cáo
Trả lời:
Đáp án: 20
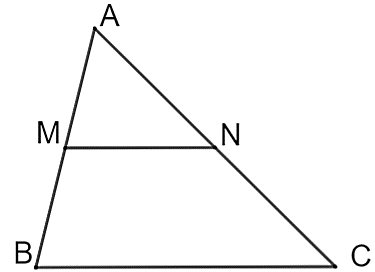
Chu vi \(\Delta ABC\) bằng \(40\;{\rm{cm}}\) nên \(AB + AC + BC = 40\;\left( {{\rm{cm}}} \right).\)
Vì \(M,\;N\) lần lượt là trung điểm của \(AB,\;AC\) nên \(AM = \frac{1}{2}AB,\;AN = \frac{1}{2}AC.\)
\(\Delta ABC\) có \(M,\;N\) lần lượt là trung điểm của \(AB,\;AC\) nên \(MN\) là đường trung bình của \(\Delta ABC.\)
Suy ra: \(MN = \frac{1}{2}BC.\)
Chu vi \(\Delta AMN\) là: \(AM + AN + MN = \frac{1}{2}\left( {AB + AC + BC} \right) = \frac{1}{2} \cdot 40 = 20\;\left( {{\rm{cm}}} \right).\)
Vậy chu vi \(\Delta AMN\) bằng \(20\;{\rm{cm}}{\rm{.}}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp án: 0,4
Các kết quả có thể xảy ra khi lập một số có ba chữ số khác nhau từ các số \(1,2,3,4,6\) là: \(5.4.3 = 60\).
Gọi \(A\) là biến cố “Số được chọn chia hết cho 3”.
Nhận thấy ta lập được 4 bộ số gồm 3 chữ số có tổng chia hết cho 3 là:
\(\left( {1;2;3} \right);{\rm{ }}\left( {1;2;6} \right);{\rm{ }}\left( {2;3;4} \right);{\rm{ }}\left( {2;4;6} \right)\).
Mỗi bộ số, ta lập được các số có ba chữ số là: \(3.2.1 = 6\) (số)
Do đó, 4 bộ số thì lập được các số có tổng chữ số chia hết cho 3 là: \(6.4 = 24\) (số)
Suy ra số kết quả thuận lợi của biến cố “Số được chọn chia hết cho 3” là: \(24\)số.
Xác suất của biến cố \(A\) là: \(\frac{{24}}{{60}} = \frac{2}{5} = 0,4.\)
Câu 2
Lời giải
Đáp án đúng là: a) Đúng. b) Sai. c) Sai. d) Đúng.
a) Các kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số lẻ”, đó là: \(1;\,\,3;\,\,5;....;\,\,37;\,\,39.\)
Do đó, có \(20\) kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số lẻ”.
Do đó, ý a) là đúng.
b) Các kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút là bình phương của một số” là:
\(1;\,\,4;\,\,9;\,\,16;\,\,25;\,\,36\).
Do đó, có 6 kết quả thuận lợi cho biến cố này.
Do đó, ý b) là sai.
c) Xác suất của biến cố “Số xuất hiện trên thẻ được rút là bình phương của một số” là: \(\frac{6}{{40}} = \frac{3}{{20}}.\)
Do đó, ý c) là sai.
d) Kết quả thuận lợi của biến cố: “Số xuất hiện trên thẻ được rút ra là lập phương của một số” là: \(1;\,\,8;\,\,27.\)
Do đó có 3 kết quả thuận lợi cho biến cố này.
Vậy xác suất của biến cố này là \(\frac{3}{{40}} = 0,075.\)
Do đó, ý d) là đúng.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.