Một tàu du lịch xuôi dòng 15 km, sau đó quay ngược lại để trở về điểm xuất phát và kết thúc chuyến đi du lịch. Biết rằng vận tốc của tàu khi nước yên lặng là 10 km/h và vận tốc của dòng nước là \(x\) km/h \(\left( {x > 0} \right)\).
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án đúng là: a) Sai. b) Sai. c) Đúng. d) Sai.
Ta có vận tốc của tàu du lịch khi nước xuôi dòng là \(x + 10\) (km/h) .
Do đó, thời gian xuôi dòng là \(\frac{{15}}{{10 + x}}\) giờ.
Do đó, ý a) sai.
Vận tốc tàu khi ngược dòng là \(10 - x\) (km/h).
Do đó, thời gian tàu ngược dòng là \(\frac{{15}}{{10 - x}}\) giờ.
Do đó, ý b) sai.
Tổng thời gian tàu chạy là \(\frac{{15}}{{10 - x}} + \frac{{15}}{{10 + x}} = \frac{{15\left( {10 + x} \right) + 15\left( {10 - x} \right)}}{{\left( {10 - x} \right)\left( {10 + x} \right)}} = \frac{{300}}{{100 - {x^2}}}\) giờ.
Do đó, ý c) là đúng.
Khi vận tốc dòng nước là 2 km/h thì thời gian tàu chạy là: \(\frac{{300}}{{100 - {2^2}}} = \frac{{25}}{8} = 3,125\) giờ.
Do đó, ý d) là sai.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Hướng dẫn giải
Đáp án đúng là: a) Đúng. b) Đúng. c) Sai. d) Đúng.
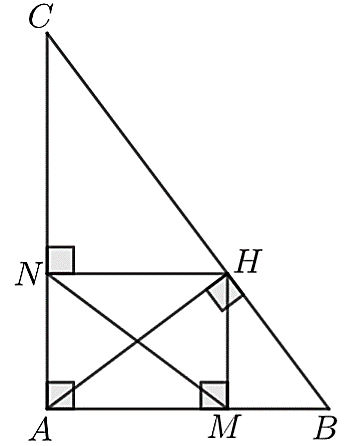
Vì \(M,\;\,N\) lần lượt là hình chiếu của \(H\) trên \(AB,\;\,AC\) nên \(HM \bot AB;\;\,HN \bot AC.\)
Do đó, \(\widehat {AMH} = \widehat {HMB} = \widehat {ANH} = \widehat {HNC} = 90^\circ .\)
Vì \(AH\) là đường cao của tam giác \(ABC\) nên \(AH \bot BC.\) Suy ra \(\widehat {AHB} = \widehat {AHC} = 90^\circ .\)
\(\Delta AHM\) và \(\Delta ABH\) có: \(\widehat {AMH} = \widehat {AHB} = 90^\circ ;\;\,\widehat {HAM}\) chung nên (g.g).
Do đó, ý a) đúng.
\(\Delta AHN\) và \(\Delta ACH\) có: \(\widehat {ANH} = \widehat {AHC} = 90^\circ ;\;\,\widehat {HAN}\) chung nên (g.g).
Do đó, \(\frac{{AH}}{{AC}} = \frac{{AN}}{{AH}}.\) Suy ra \(A{H^2} = AN \cdot AC.\)
Do đó, ý b) đúng.
Theo a) ta có: (g.g) nên \(\frac{{AM}}{{AH}} = \frac{{AH}}{{AB}}.\) Suy ra \(AM \cdot AB = A{H^2}.\)
Mà \(A{H^2} = AN \cdot AC\) nên \(AM \cdot AB = AN \cdot AC.\)
Do đó, ý c) sai.
Vì \(AM \cdot AB = AN \cdot AC\) nên \(\frac{{AM}}{{AC}} = \frac{{AN}}{{AB}}.\)
\(\Delta ANM\) và \(\Delta ABC\) có: \(\frac{{AM}}{{AC}} = \frac{{AN}}{{AB}};\;\,\widehat {NAM} = \widehat {BAC} = 90^\circ \) chung nên (c.g.c).
Do đó, ý d) đúng.
Lời giải
Hướng dẫn giải
Đáp án: 16
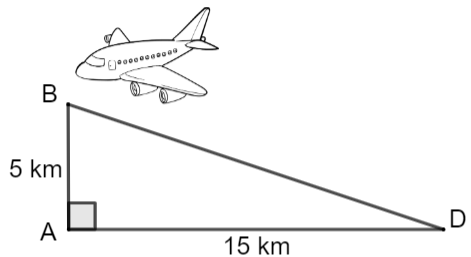
Áp dụng định lý Pythagore vào \(\Delta ABD\) vuông tại \(A\) ta có:
\(B{D^2} = A{B^2} + A{D^2} = {5^2} + {15^2} = 250\) nên \(BD = \sqrt {250} \approx 16\;{\rm{km}}{\rm{.}}\)
Vậy khoảng cách từ vị trí máy bay đến vị trí \(D\) của sân bay là khoảng \(16\;{\rm{km}}{\rm{.}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.