Trong một cửa hàng bán thực phẩm, bác Lan nhìn thấy cô bán hàng dùng một chiếc cân đĩa. Bên đĩa thứ nhất, cô đặt hai quả cân, mỗi quả nặng \(500\;\,{\rm{g,}}\) bên đĩa thứ hai, cô đặt hai gói hàng cùng cân nặng \(x\;\,\left( {\rm{g}} \right)\) và bốn quả cân nhỏ, mỗi quả cân nặng \(50\;{\rm{g}}{\rm{.}}\) Bác Lan thấy cân thăng bằng.
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án đúng là: a) Sai. b) Đúng. c) Sai. d) Đúng.
Đĩa thứ nhất nặng: \(2 \cdot 500 = 1\;\,000\;\,\left( {\rm{g}} \right){\rm{.}}\) Vậy đĩa thứ nhất nặng \(1\;\,000\;{\rm{g}}{\rm{.}}\)
Do đó, ý a) là sai.
Đĩa thứ hai nặng: \(2x + 4 \cdot 50 = 2x + 200\;\,\left( {\rm{g}} \right).\) Vậy đĩa thứ hai nặng \(2x + 200\;\,\left( {\rm{g}} \right).\)
Do đó, ý b) là đúng.
Phương trình biểu thị sự thăng bằng của cân là \(2x + 200 = 1\;000.\)
Do đó, ý c) là sai.
Giải phương trình: \(2x + 200 = 1\;000\)
\(2x = 800\)
\(x = 400.\)
Vậy mỗi gói hàng nặng \(400\;\,{\rm{g}}{\rm{.}}\)
Do đó, ý d) là đúng.x
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Hướng dẫn giải
Đáp án đúng là: a) Đúng. b) Đúng. c) Sai. d) Đúng.
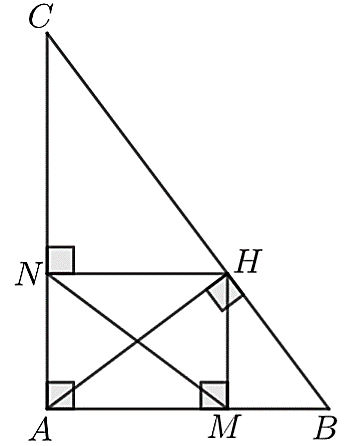
Vì \(M,\;\,N\) lần lượt là hình chiếu của \(H\) trên \(AB,\;\,AC\) nên \(HM \bot AB;\;\,HN \bot AC.\)
Do đó, \(\widehat {AMH} = \widehat {HMB} = \widehat {ANH} = \widehat {HNC} = 90^\circ .\)
Vì \(AH\) là đường cao của tam giác \(ABC\) nên \(AH \bot BC.\) Suy ra \(\widehat {AHB} = \widehat {AHC} = 90^\circ .\)
\(\Delta AHM\) và \(\Delta ABH\) có: \(\widehat {AMH} = \widehat {AHB} = 90^\circ ;\;\,\widehat {HAM}\) chung nên (g.g).
Do đó, ý a) đúng.
\(\Delta AHN\) và \(\Delta ACH\) có: \(\widehat {ANH} = \widehat {AHC} = 90^\circ ;\;\,\widehat {HAN}\) chung nên (g.g).
Do đó, \(\frac{{AH}}{{AC}} = \frac{{AN}}{{AH}}.\) Suy ra \(A{H^2} = AN \cdot AC.\)
Do đó, ý b) đúng.
Theo a) ta có: (g.g) nên \(\frac{{AM}}{{AH}} = \frac{{AH}}{{AB}}.\) Suy ra \(AM \cdot AB = A{H^2}.\)
Mà \(A{H^2} = AN \cdot AC\) nên \(AM \cdot AB = AN \cdot AC.\)
Do đó, ý c) sai.
Vì \(AM \cdot AB = AN \cdot AC\) nên \(\frac{{AM}}{{AC}} = \frac{{AN}}{{AB}}.\)
\(\Delta ANM\) và \(\Delta ABC\) có: \(\frac{{AM}}{{AC}} = \frac{{AN}}{{AB}};\;\,\widehat {NAM} = \widehat {BAC} = 90^\circ \) chung nên (c.g.c).
Do đó, ý d) đúng.
Lời giải
Hướng dẫn giải
Đáp án: 16
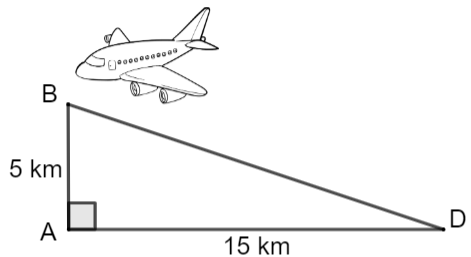
Áp dụng định lý Pythagore vào \(\Delta ABD\) vuông tại \(A\) ta có:
\(B{D^2} = A{B^2} + A{D^2} = {5^2} + {15^2} = 250\) nên \(BD = \sqrt {250} \approx 16\;{\rm{km}}{\rm{.}}\)
Vậy khoảng cách từ vị trí máy bay đến vị trí \(D\) của sân bay là khoảng \(16\;{\rm{km}}{\rm{.}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.