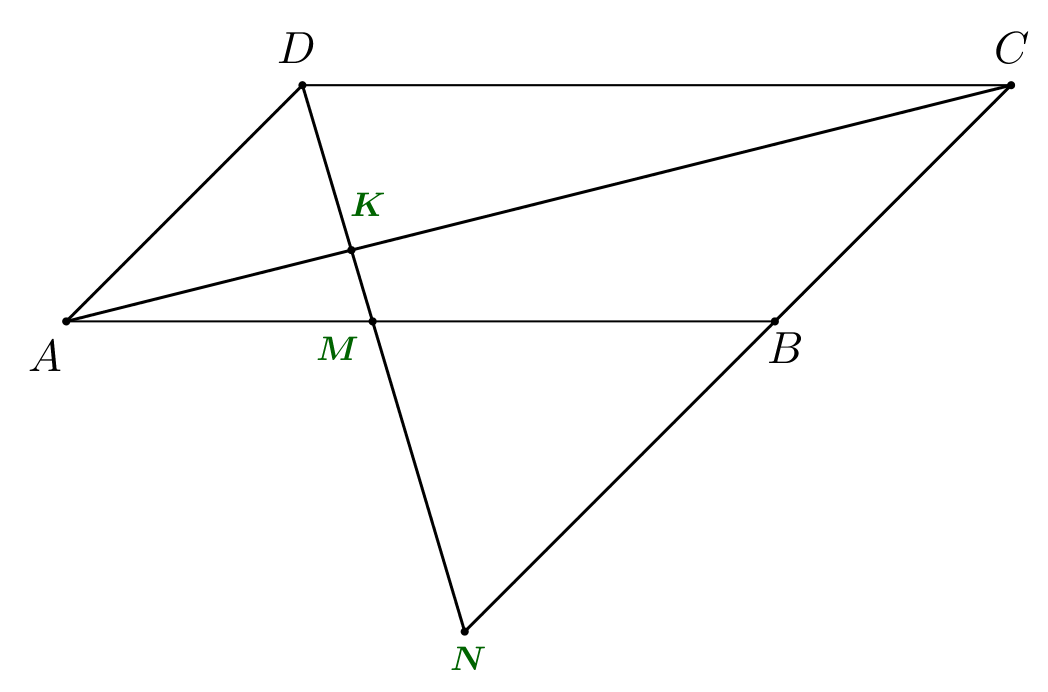
Cho hình bình hành \(ABCD\;\left( {AB > BC} \right),\) điểm \(M \in AB.\) Đường thẳng \(DM\) cắt \(AC\) ở \(K,\) cắt \(BC\) ở \(N.\)
a) Chứng minh
b) Chứng minh \(\frac{{KM}}{{KD}} = \frac{{KA}}{{KC}}.\) Từ đó chứng minh \(K{D^2} = KM \cdot KN.\)
c) Cho \(AB = 10\) cm, \(AD = 9\) cm, \(AM = 6\) cm. Tính \(CN.\)
Cho hình bình hành \(ABCD\;\left( {AB > BC} \right),\) điểm \(M \in AB.\) Đường thẳng \(DM\) cắt \(AC\) ở \(K,\) cắt \(BC\) ở \(N.\)
a) Chứng minh
b) Chứng minh \(\frac{{KM}}{{KD}} = \frac{{KA}}{{KC}}.\) Từ đó chứng minh \(K{D^2} = KM \cdot KN.\)
c) Cho \(AB = 10\) cm, \(AD = 9\) cm, \(AM = 6\) cm. Tính \(CN.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
|
a) Do \(ABCD\) là hình bình hành nên \(AB\,{\rm{//}}\,CD\) và \(AD\,{\rm{//}}\,BC.\) Xét \(\Delta ADK\) có \(AD\,{\rm{//}}\,CN\) (do \(AD\,{\rm{//}}\,BC)\) nên (g.g). b) Xét \(\Delta KAM\) có \(AM\,{\rm{//}}\,CD\) (do \(AB\,{\rm{//}}\,CD)\) nên (g.g). Suy ra \(\frac{{KM}}{{KD}} = \frac{{KA}}{{KC}}\) (tỉ số cạnh tương ứng). |
|
Mà (câu a) nên \(\frac{{KD}}{{KN}} = \frac{{AK}}{{CK}}\) (tỉ số cạnh tương ứng).
Suy ra \(\frac{{KD}}{{KN}} = \frac{{KM}}{{KD}}\) nên \(K{D^2} = KM \cdot KN.\)
c) Do nên \(\frac{{AK}}{{CK}} = \frac{{AD}}{{CN}}\) (tỉ số cạnh tương ứng).
Do nên \(\frac{{AK}}{{CK}} = \frac{{AM}}{{CD}}\) (tỉ số cạnh tương ứng).
Suy ra \(\frac{{AD}}{{CN}} = \frac{{AM}}{{CD}}\) hay \(\frac{9}{{CN}} = \frac{6}{{10}},\) do đó \(CN = \frac{{9 \cdot 10}}{6} = 15\) (cm).
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
|
a) Xét \(\Delta ADC\) và \(\Delta BEC\) có: \(\widehat {ADC} = \widehat {BEC} = 90^\circ \) và \(\widehat {ACB}\) là góc chung. Do đó (g.g). b) Xét \(\Delta HEA\) và \(\Delta HDB\) có: \(\widehat {HEA} = \widehat {HDB} = 90^\circ \) và \(\widehat {AHE} = \widehat {BHD}\) (đối đỉnh) Do đó (g.g). |
|
Suy ra \(\frac{{HE}}{{HD}} = \frac{{HA}}{{HB}}\) (tỉ số cạnh tương ứng) nên \(HE \cdot HB = HA \cdot HD.\)
c) Vì \(H\) là giao điểm của hai đường cao \(AD,\,\,BE\) của tam giác \(ABC\) nên \(H\) là trực tâm của tam giác, nên \(CH \bot AB,\) hay \(\widehat {AFC} = 90^\circ .\)
Xét \(\Delta AFH\) và \(\Delta ADB\) có:
\(\widehat {AFH} = \widehat {ADB} = 90^\circ \) và \(\widehat {DAB}\) là góc chung
Do đó (g.g).
Suy ra \(\frac{{AF}}{{AD}} = \frac{{AH}}{{AB}}\) (tỉ số cạnh tương ứng) nên \(AF \cdot AB = AD \cdot AH.\)
d) Ta có \(\frac{{{S_{\Delta BHC}}}}{{{S_{\Delta ABC}}}} = \frac{{\frac{1}{2}HD \cdot BC}}{{\frac{1}{2}AD \cdot BC}} = \frac{{HD}}{{AD}}.\)
Tương tự: \(\frac{{{S_{\Delta AHC}}}}{{{S_{\Delta ABC}}}} = \frac{{HE}}{{BE}};\) \(\frac{{{S_{\Delta AHB}}}}{{{S_{\Delta ABC}}}} = \frac{{HF}}{{CF}}.\)
Khi đó \(\frac{{HD}}{{AD}} + \frac{{HE}}{{BE}} + \frac{{HF}}{{CF}}\)\[ = \frac{{{S_{\Delta AHB}} + {S_{\Delta BHC}} + {S_{\Delta CHA}}}}{{{S_{\Delta ABC}}}} = \frac{{{S_{\Delta ABC}}}}{{{S_{\Delta ABC}}}} = 1.\]
Lời giải
Hướng dẫn giải
|
a) Xét \(\Delta ABE\) và \(\Delta ADC\) có: \(\widehat {BAE}\) là góc chung; \[\frac{{AB}}{{AD}} = \frac{{AE}}{{AC}}\,\,\left( {\frac{8}{{10}} = \frac{{12}}{{15}} = \frac{4}{5}} \right).\] Do đó (c.g.c). b) Vì (câu a) nên \(\frac{{AB}}{{AD}} = \frac{{BE}}{{DC}}\) Suy ra \(AB \cdot DC = AD \cdot BE.\) Do đó \(DC = \frac{{AD \cdot BE}}{{AB}} = \frac{{10 \cdot 10}}{8} = 12,5{\rm{\;cm}}.\) |
|
c) Vì (câu a) nên \(\widehat {AEB} = \widehat {ACD}\) (hai góc tương ứng).
Xét \(\Delta CBI\) và \(\Delta EDI\) có:
\(\widehat {BCI} = \widehat {DEI}\) (do \(\widehat {AEB} = \widehat {ACD})\) và \(\widehat {BIC} = \widehat {DIE}\) (hai góc đối đỉnh)
Do đó (g.g).
Suy ra \(\frac{{IC}}{{IE}} = \frac{{IB}}{{ID}}\) (tỉ số cạnh tương ứng) nên \[IB \cdot IE = ID \cdot IC.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập