Một lớp học có 40 học sinh trong đó có 25 học sinh thích môn Toán, 20 học sinh thích môn Ngữ văn và 12 học sinh thích cả hai môn Ngữ văn và Toán. Tính xác suất để chọn được một học sinh thích môn Ngữ văn mà không thích môn Toán.

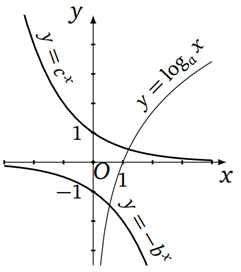
Từ hình vẽ ta có: *) \[a > 1\]. Vì hàm \[y = {\log _a}x\] đồng biến: Tính từ trái qua phải đồ thị có dạng đi lên.

*) Lấy đối xứng đồ thị hàm số \[y =  - {b^x}\] qua trục \[Ox\]ta được đồ thị hàm số \[y = {b^x}\]

                               là hàm đồng biến, nên \[\,b > 1\].

*) \[0 < c < 1.\]Vì hàm \[y = {c^x}\] nghịch biến: Tính từ trái qua phải đt có dạng đi xuống.

Do đó:

\[\left. \begin{array}{l}a + b > 2\\0 < c < 1\end{array} \right\} \Rightarrow {\log _c}\left( {a + b} \right) < {\log _c}2 \Rightarrow \]Đáp án a sai.

\[\left. \begin{array}{l}0 < c < 1\\ab > 1\end{array} \right\} \Rightarrow {\log _{ab}}c < {\log _{ab}}1 = 0 \Rightarrow \]Đáp án b sai.

\[\left. \begin{array}{l}\frac{b}{c} > 1\\a > 1\end{array} \right\} \Rightarrow {\log _a}\frac{b}{c} > {\log _a}1 = 0 \Rightarrow \]Đáp án c đúng.

\[\left. \begin{array}{l}\frac{a}{c} > 1\\b > 1\end{array} \right\} \Rightarrow {\log _b}\frac{a}{c} > {\log _b}1 = 0 \Rightarrow \]Đáp án d sai.

Trả lời: 3 m/s.                

Lời giải

Ta có: \(v = S' =  - 3{t^2} + 6t\).

\({v_{\max }} \Leftrightarrow t = \frac{{ - b}}{{2a}} = 1\left( s \right)\)

\( \Rightarrow {v_{\max }} = v\left( 1 \right) = 3m/s\).