Cho hình chóp S.ABCD có đáy ABCD là hình thoi và \(AB = BD = a,SA = a\sqrt 3 ,SA \bot (ABCD)\). Gọi \(M\) là điểm trên cạnh SB sao cho \(BM = \frac{2}{3}SB\). Giả sử \(N\) là điểm di động trên trên cạnh AD. Tìm vị trí điểm \(N\) để \(BN \bot DM\)?
Cho hình chóp S.ABCD có đáy ABCD là hình thoi và \(AB = BD = a,SA = a\sqrt 3 ,SA \bot (ABCD)\). Gọi \(M\) là điểm trên cạnh SB sao cho \(BM = \frac{2}{3}SB\). Giả sử \(N\) là điểm di động trên trên cạnh AD. Tìm vị trí điểm \(N\) để \(BN \bot DM\)?
A. \(N\) nằm trên cạnh AD sao cho \(AN = \frac{3}{5}AD\)
B. \(N\) nằm trên cạnh AD sao cho \(AN = \frac{2}{5}AD\)
C. \(N\) nằm trên cạnh AD sao cho \(AN = \frac{4}{5}AD\)
D. \(N\) nằm trên cạnh AD sao cho \(AN = \frac{3}{4}AD\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là B
Phương pháp giải
Phân tích vecto.
Lời giải
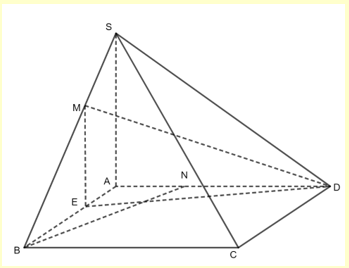
Vẽ , do đó \(DM \bot BN \Leftrightarrow DE \bot BN\). Đặt \(AN = xAD\)
Ta có : \(\overrightarrow {DE} = \overrightarrow {DA} + \overrightarrow {AE} = - \overrightarrow {AD} + \frac{1}{3}\overrightarrow {AB} \)
\(\overrightarrow {BN} = - \overrightarrow {AB} + \overrightarrow {AN} = - \overrightarrow {AB} + x\overrightarrow {AD} \)
Vì \(BN \bot DE \Rightarrow (3\overrightarrow {AD} - \overrightarrow {AB} )(\overrightarrow {AB} - x\overrightarrow {AD} ) = 0\)
\( \Leftrightarrow - 3xA{D^2} - A{B^2} + (3 + x)\overrightarrow {AB} .\overrightarrow {AD} = 0\)
Vì tam giác ABD đều nên: \(\overrightarrow {AB} .\overrightarrow {AD} = AB.AD.\cos \widehat {BAD} = a.a.\cos {60^\circ } = \frac{{{a^2}}}{2}\)
\( \Rightarrow - 3a{x^2} - {a^2} + \frac{{{a^2}(3 + x)}}{2} = 0 \Leftrightarrow x = \frac{2}{5} \Rightarrow AN = \frac{2}{5}AD\)
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. sang phải 5cm.
B. sang trái 5cm.
C. sang phải 10cm.
D. sang trái 10cm.
Lời giải
Đáp án đúng là D
Phương pháp giải
Sử dụng công thức tính tính thể tích: V = hS
Xác định các thông số trạng thái.
Áp dụng công thức định luật Boyle.
Lời giải
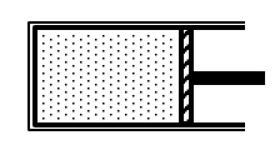
Xét trạng thái 1: \(\left\{ {\begin{array}{*{20}{l}}{{p_1}}\\{{V_1} = {h_1}S}\end{array}} \right.\)
Xét trạng thái 2: \(\left\{ {\begin{array}{*{20}{l}}{{p_2} = 3{p_1}}\\{{V_2} = {h_2}S}\end{array}} \right.\)
Quá trình đẳng nhiệt diễn ra nên ta có: \({p_1}{V_1} = {p_2}{V_2}\)
\(\begin{array}{l} \Rightarrow {p_1}{h_1}S = 3{p_1}{h_2}S\\ \Rightarrow {h_1} = 2{h_2}\\ \Rightarrow {h_2} = \frac{{{h_1}}}{3} = 5\;{\rm{cm}}\end{array}\)
\( \Rightarrow \) pitong dịch sang trái 10 cm.
Câu 2
A. Hiện tượng đồng âm
B. Hiện tượng trái nghĩa
C. Hiện tượng đồng nghĩa
D. Hiện tượng đa nghĩa
Lời giải
Đáp án đúng là A
Phương pháp giải
Căn cứ vào kiến thức về từ đồng âm, từ nhiều nghĩa.
Nội dung/ Thông điệp
Lời giải
- Từ “đường” trong bài thơ trên là con đường để đi lại, con đường giao thông.
- Từ “đường” trong cụm từ “ngọt như đường” có nghĩa là đường thực phẩm, đường dùng trong nấu ăn, pha chế, có vị ngọt.
- Hai từ “đường” khác biệt hoàn toàn về nghĩa, chỉ có âm giống nhau, đây là hiện tượng từ đồng âm.
Câu 3
A. Nhiệt độ trung bình năm giảm dần từ Nam ra Bắc do nước ta lãnh thổ nước ta hẹp ngang, nhiều đồi núi.
B. Biên độ nhiệt năm giảm dần từ Nam ra Bắc do miền Nam không chịu ảnh hưởng của gió mùa Đông Bắc.
C. Bãi Cháy có biên độ nhiệt trung bình năm cao do vị trí địa lí và ảnh hưởng của gió mùa mùa đông.
D. Chênh lệch nhiệt độ trung bình năm giữa Cà Mau và Đà Nẵng là 1,4°C do đều nằm ở vùng khí hậu phía Nam.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Lào cao hơn Cam-pu-chia và thấp hơn In-đô-nê-xi-a.
B. In-đô-nê-xi-a cao hơn Cam-pu-chia và thấp hơn Lào.
C. Cam-pu-chia cao hơn In-đô-nê-xi-a và cao hơn Lào.
D. Cam-pu-chia cao hơn In-đô-nê-xi-a và thấp hơn Lào.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. (I), (II), (III)
B. (II), (III), (IV)
C. (I), (III), (IV)
D. (I), (II), (IV)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập