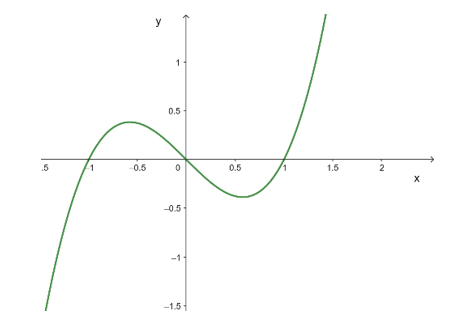
Cho hàm số \(y = f(x)\) có đạo hàm \(\forall x \in \mathbb{R}\), hàm số \({f^\prime }(x) = {x^3} + a{x^2} + bx + c\) có đồ thị như hình vẽ.

Số điểm cực trị của hàm số: \(y = f\left[ {{f^\prime }(x)} \right]\) là:

Đáp án đúng là B

Phương pháp giải

Sử dụng tương giao đồ thị

Lời giải

Xét hàm số \(y = f\left( {{x^2} - 3x + m} \right)\) có

\({y^\prime } = (2x - 3).{f^\prime }\left( {{x^2} - 3x + m} \right)\)

\({y^\prime } = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{2x - 3 = 0}\\{{f^\prime }\left( {{x^2} - 3x + m} \right) = 0}\end{array}} \right.\)

Để hàm số \(y = f\left( {{x^2} - 3x + m} \right)\) có nhiều cực trị nhất thì phương trình \({f^\prime }\left( {{x^2} - 3x + m} \right) = 0\) có nhiều nghiệm bội lẻ khác \(\frac{3}{2}\) nhất.

Xét phương trình: \({f^\prime }\left( {{x^2} - 3x + m} \right) = 0 \Leftrightarrow \left( {{x^2} - 3x + m + 3} \right)\left( {{x^2} - 3x + m - 4} \right) = 0\)

\( \Rightarrow \left[ {\begin{array}{*{20}{l}}{{x^2} - 3x = - m - 3}\\{{x^2} - 3x = 4 - m}\end{array}} \right.\)

Xét hàm số : \(h(x) = {x^2} - 3x\)

\({h^\prime }(x) = 2x - 3,{h^\prime } = 0 \Rightarrow x = \frac{3}{2}\)

Bảng biến thiên hàm số \(h(x) = {x^2} - 3x\)

Để \({f^\prime }\left( {{x^2} - 3x + m} \right) = 0 \Leftrightarrow \left( {{x^2} - 3x + m + 3} \right)\left( {{x^2} - 3x + m - 4} \right) = 0\) có nhiều nghiệm bội lẻ nhất \( \Rightarrow \left[ {\begin{array}{*{20}{l}}{{x^2} - 3x = - m - 3}\\{{x^2} - 3x = 4 - m}\end{array}} \right.\) có nhiều nghiệm bội lẻ nhất

Số nghiệm của hai phương trình này là số giao điểm của đồ thị hàm số \(h(x) = {x^2} - 3x\) và các đường thẳng \(y = - m - 3\) và \(y = 4 - m\)

Dựa vào bảng biến thiên của hàm số \(h(x) = {x^2} - 3x \Rightarrow \left[ {\begin{array}{*{20}{l}}{ - m - 3 > \frac{{ - 9}}{4}}\\{4 - m > \frac{{ - 9}}{4}}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m < \frac{{ - 3}}{4}}\\{m < \frac{{25}}{4}}\end{array}} \right.} \right.\)

Mà \(m \in [ - 10;5]\), kết hợp các điều kiện \( \Rightarrow m \in \left( {\frac{{ - 3}}{4};5} \right],m \in \mathbb{Z} \Rightarrow m \in \{ 0;1;2;3;4;5\} \)

Vậy tổng các giá trị nguyên của \(m\) thỏa mãn yêu cầu bài toán là: 15

Đáp án đúng là D

Phương pháp giải

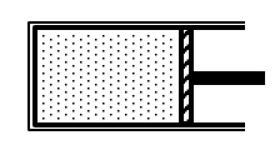
Sử dụng công thức tính tính thể tích: V = hS

Xác định các thông số trạng thái.

Áp dụng công thức định luật Boyle.

Lời giải

Xét trạng thái 1: \(\left\{ {\begin{array}{*{20}{l}}{{p_1}}\\{{V_1} = {h_1}S}\end{array}} \right.\)

Xét trạng thái 2: \(\left\{ {\begin{array}{*{20}{l}}{{p_2} = 3{p_1}}\\{{V_2} = {h_2}S}\end{array}} \right.\)

Quá trình đẳng nhiệt diễn ra nên ta có: \({p_1}{V_1} = {p_2}{V_2}\)

\(\begin{array}{l} \Rightarrow {p_1}{h_1}S = 3{p_1}{h_2}S\\ \Rightarrow {h_1} = 2{h_2}\\ \Rightarrow {h_2} = \frac{{{h_1}}}{3} = 5\;{\rm{cm}}\end{array}\)

\( \Rightarrow \) pitong dịch sang trái 10 cm.