Đọc đoạn thơ sau và trả lời câu hỏi:

Mùa thu nay sao bão giông nhiều

Những cửa sổ con tàu chẳng đóng

Dải đồng hoang và đại ngàn tối sẫm

Em lạc loài giữa sâu thẳm rừng anh…

(Xuân Quỳnh, Tự hát, dẫn theo thivien.net)

Ý nghĩa nào KHÔNG được suy ra từ đoạn thơ trên?

 

Đáp án đúng là D

Phương pháp giải

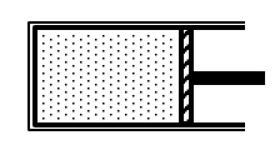
Sử dụng công thức tính tính thể tích: V = hS

Xác định các thông số trạng thái.

Áp dụng công thức định luật Boyle.

Lời giải

Xét trạng thái 1: \(\left\{ {\begin{array}{*{20}{l}}{{p_1}}\\{{V_1} = {h_1}S}\end{array}} \right.\)

Xét trạng thái 2: \(\left\{ {\begin{array}{*{20}{l}}{{p_2} = 3{p_1}}\\{{V_2} = {h_2}S}\end{array}} \right.\)

Quá trình đẳng nhiệt diễn ra nên ta có: \({p_1}{V_1} = {p_2}{V_2}\)

\(\begin{array}{l} \Rightarrow {p_1}{h_1}S = 3{p_1}{h_2}S\\ \Rightarrow {h_1} = 2{h_2}\\ \Rightarrow {h_2} = \frac{{{h_1}}}{3} = 5\;{\rm{cm}}\end{array}\)

\( \Rightarrow \) pitong dịch sang trái 10 cm.

Đáp án đúng là B

Phương pháp giải

Sử dụng tương giao đồ thị

Lời giải

Xét hàm số \(y = f\left( {{x^2} - 3x + m} \right)\) có

\({y^\prime } = (2x - 3).{f^\prime }\left( {{x^2} - 3x + m} \right)\)

\({y^\prime } = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{2x - 3 = 0}\\{{f^\prime }\left( {{x^2} - 3x + m} \right) = 0}\end{array}} \right.\)

Để hàm số \(y = f\left( {{x^2} - 3x + m} \right)\) có nhiều cực trị nhất thì phương trình \({f^\prime }\left( {{x^2} - 3x + m} \right) = 0\) có nhiều nghiệm bội lẻ khác \(\frac{3}{2}\) nhất.

Xét phương trình: \({f^\prime }\left( {{x^2} - 3x + m} \right) = 0 \Leftrightarrow \left( {{x^2} - 3x + m + 3} \right)\left( {{x^2} - 3x + m - 4} \right) = 0\)

\( \Rightarrow \left[ {\begin{array}{*{20}{l}}{{x^2} - 3x = - m - 3}\\{{x^2} - 3x = 4 - m}\end{array}} \right.\)

Xét hàm số : \(h(x) = {x^2} - 3x\)

\({h^\prime }(x) = 2x - 3,{h^\prime } = 0 \Rightarrow x = \frac{3}{2}\)

Bảng biến thiên hàm số \(h(x) = {x^2} - 3x\)

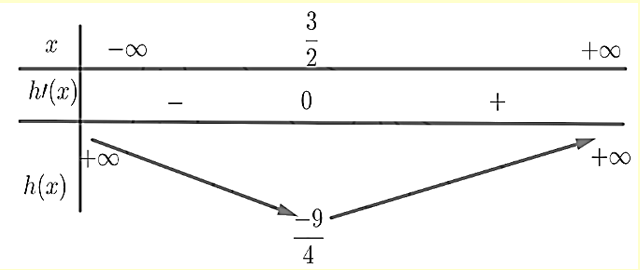
Để \({f^\prime }\left( {{x^2} - 3x + m} \right) = 0 \Leftrightarrow \left( {{x^2} - 3x + m + 3} \right)\left( {{x^2} - 3x + m - 4} \right) = 0\) có nhiều nghiệm bội lẻ nhất \( \Rightarrow \left[ {\begin{array}{*{20}{l}}{{x^2} - 3x = - m - 3}\\{{x^2} - 3x = 4 - m}\end{array}} \right.\) có nhiều nghiệm bội lẻ nhất

Số nghiệm của hai phương trình này là số giao điểm của đồ thị hàm số \(h(x) = {x^2} - 3x\) và các đường thẳng \(y = - m - 3\) và \(y = 4 - m\)

Dựa vào bảng biến thiên của hàm số \(h(x) = {x^2} - 3x \Rightarrow \left[ {\begin{array}{*{20}{l}}{ - m - 3 > \frac{{ - 9}}{4}}\\{4 - m > \frac{{ - 9}}{4}}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m < \frac{{ - 3}}{4}}\\{m < \frac{{25}}{4}}\end{array}} \right.} \right.\)

Mà \(m \in [ - 10;5]\), kết hợp các điều kiện \( \Rightarrow m \in \left( {\frac{{ - 3}}{4};5} \right],m \in \mathbb{Z} \Rightarrow m \in \{ 0;1;2;3;4;5\} \)

Vậy tổng các giá trị nguyên của \(m\) thỏa mãn yêu cầu bài toán là: 15