Đọc đoạn trích sau và trả lời câu hỏi:

     Vang bóng một thời chứa đựng nội dung của bất trắc, thường trực đi trên sợi dây căng giữa hai vùng sáng tối. Trong Chữ người tử tù, cái tối tăm, tàn nhẫn, lừa lọc, thô bạo của đề lao đối diện với ánh sáng của giải lụa bạch tinh khiết căng lên dưới nét chữ thần sầu của người tử tù. Càng làm nổi sự sang trọng của hai nhân cách đối nghịch: một cai ngục và một anh hùng. Ðem không khí âm u tăm tối của nghề cai ngục đối chất với nỗi khát vọng nghệ thuật và lòng quý trọng nhân tài trong tâm hồn hắn. Ðem cái chết trước mắt của người tử tù đối diện với nét chữ sống mãi của người tài tử. Ðặt cái gông trên cổ Huấn Cao, kẻ mang trong người chất tự do, ngang tàng, vùng vẫy, không khuất phục của Bá Quát. Làm cho những sự nham hiểm, hèn mọn, hút trộm máu người của bọn rệp phải rụng như mưa dưới cái lắc mạnh của người anh hùng…

(Thuỵ Khuê, Thi pháp Nguyễn Tuân, 2003)

Nội dung chính của đoạn trích trên là gì?

  

Đáp án đúng là D

Phương pháp giải

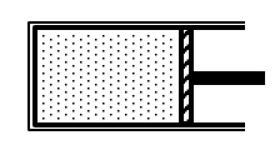
Sử dụng công thức tính tính thể tích: V = hS

Xác định các thông số trạng thái.

Áp dụng công thức định luật Boyle.

Lời giải

Xét trạng thái 1: \(\left\{ {\begin{array}{*{20}{l}}{{p_1}}\\{{V_1} = {h_1}S}\end{array}} \right.\)

Xét trạng thái 2: \(\left\{ {\begin{array}{*{20}{l}}{{p_2} = 3{p_1}}\\{{V_2} = {h_2}S}\end{array}} \right.\)

Quá trình đẳng nhiệt diễn ra nên ta có: \({p_1}{V_1} = {p_2}{V_2}\)

\(\begin{array}{l} \Rightarrow {p_1}{h_1}S = 3{p_1}{h_2}S\\ \Rightarrow {h_1} = 2{h_2}\\ \Rightarrow {h_2} = \frac{{{h_1}}}{3} = 5\;{\rm{cm}}\end{array}\)

\( \Rightarrow \) pitong dịch sang trái 10 cm.

Đáp án đúng là B

Phương pháp giải

Sử dụng tương giao đồ thị

Lời giải

Xét hàm số \(y = f\left( {{x^2} - 3x + m} \right)\) có

\({y^\prime } = (2x - 3).{f^\prime }\left( {{x^2} - 3x + m} \right)\)

\({y^\prime } = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{2x - 3 = 0}\\{{f^\prime }\left( {{x^2} - 3x + m} \right) = 0}\end{array}} \right.\)

Để hàm số \(y = f\left( {{x^2} - 3x + m} \right)\) có nhiều cực trị nhất thì phương trình \({f^\prime }\left( {{x^2} - 3x + m} \right) = 0\) có nhiều nghiệm bội lẻ khác \(\frac{3}{2}\) nhất.

Xét phương trình: \({f^\prime }\left( {{x^2} - 3x + m} \right) = 0 \Leftrightarrow \left( {{x^2} - 3x + m + 3} \right)\left( {{x^2} - 3x + m - 4} \right) = 0\)

\( \Rightarrow \left[ {\begin{array}{*{20}{l}}{{x^2} - 3x = - m - 3}\\{{x^2} - 3x = 4 - m}\end{array}} \right.\)

Xét hàm số : \(h(x) = {x^2} - 3x\)

\({h^\prime }(x) = 2x - 3,{h^\prime } = 0 \Rightarrow x = \frac{3}{2}\)

Bảng biến thiên hàm số \(h(x) = {x^2} - 3x\)

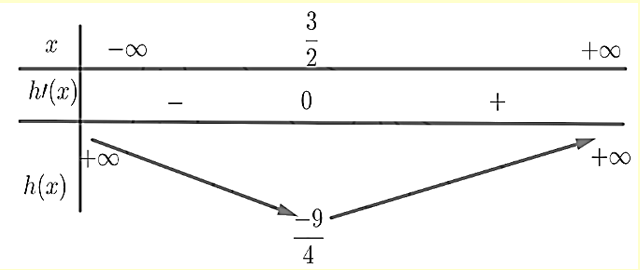
Để \({f^\prime }\left( {{x^2} - 3x + m} \right) = 0 \Leftrightarrow \left( {{x^2} - 3x + m + 3} \right)\left( {{x^2} - 3x + m - 4} \right) = 0\) có nhiều nghiệm bội lẻ nhất \( \Rightarrow \left[ {\begin{array}{*{20}{l}}{{x^2} - 3x = - m - 3}\\{{x^2} - 3x = 4 - m}\end{array}} \right.\) có nhiều nghiệm bội lẻ nhất

Số nghiệm của hai phương trình này là số giao điểm của đồ thị hàm số \(h(x) = {x^2} - 3x\) và các đường thẳng \(y = - m - 3\) và \(y = 4 - m\)

Dựa vào bảng biến thiên của hàm số \(h(x) = {x^2} - 3x \Rightarrow \left[ {\begin{array}{*{20}{l}}{ - m - 3 > \frac{{ - 9}}{4}}\\{4 - m > \frac{{ - 9}}{4}}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m < \frac{{ - 3}}{4}}\\{m < \frac{{25}}{4}}\end{array}} \right.} \right.\)

Mà \(m \in [ - 10;5]\), kết hợp các điều kiện \( \Rightarrow m \in \left( {\frac{{ - 3}}{4};5} \right],m \in \mathbb{Z} \Rightarrow m \in \{ 0;1;2;3;4;5\} \)

Vậy tổng các giá trị nguyên của \(m\) thỏa mãn yêu cầu bài toán là: 15