Đọc đoạn trích sau và trả lời câu hỏi:

Tiến sĩ Aron và nhóm của ông đã sử dụng một kính hiển vi điện tử quét để tìm hiểu về lông của kiến bạc Sahara (tên khoa học là Cataglyphis bombycina), xem điều gì sẽ xảy ra khi ánh nắng tấn công chúng. Họ cũng so sánh những con kiến bình thường với những con đã bị cạo lông để đánh giá cách ánh sáng dội lại và những con kiến bị nóng lên nhanh như thế nào dưới ánh sáng Mặt trời mô phỏng. Họ nhận thấy, những con kiến bình thường có thể phản xạ ánh sáng gấp 10 lần so với những con đã cạo lông, và có thể giữ cơ thể mát hơn đến 2 độ C dưới ánh Mặt trời mô phỏng. Kính hiển vi công suất cao tiết lộ rằng mỗi sợi lông của chú kiến có bề mặt gợn sóng và một tam giác cắt ngang. Giống như một lăng kính, các sợi lông ở lớp sau đó có thể phản xạ ánh sáng, các tia chiếu vào từng sợi đều chịu sự phản xạ nội toàn, bật khỏi những sợi lông cuối cùng thay vì truyền qua nó. Hiệu ứng gương cho phép loài kiến này làm bóng màu bạc của nó, giúp ích cho việc ngụy trang, hỗ trợ trong thông tin liên lạc giữa các con kiến, và làm giảm sự hấp thụ nhiệt từ ánh sáng Mặt trời. Cuối cùng giúp những con kiến khỏi bị thiêu đốt. Trong khi nhiều loài côn trùng và động vật ở sa mạc Sahara phải ra ngoài kiếm ăn vào ban đêm để tránh ánh nắng Mặt trời thì kiến bạc Sahara lại tung tăng được vào ban ngày. Chúng không có nỗi sợ hãi của các loài khác.

(Bí mật của loài kiến sống ung dung tự tại ở sa mạc Sahara, Theo Khoahoc.tv, ngày 19/10/2024)

Vì sao kiến bạc Sahara có thể kiếm ăn vào ban ngày?

  

Đáp án đúng là D

Phương pháp giải

Sử dụng công thức tính tính thể tích: V = hS

Xác định các thông số trạng thái.

Áp dụng công thức định luật Boyle.

Lời giải

Xét trạng thái 1: \(\left\{ {\begin{array}{*{20}{l}}{{p_1}}\\{{V_1} = {h_1}S}\end{array}} \right.\)

Xét trạng thái 2: \(\left\{ {\begin{array}{*{20}{l}}{{p_2} = 3{p_1}}\\{{V_2} = {h_2}S}\end{array}} \right.\)

Quá trình đẳng nhiệt diễn ra nên ta có: \({p_1}{V_1} = {p_2}{V_2}\)

\(\begin{array}{l} \Rightarrow {p_1}{h_1}S = 3{p_1}{h_2}S\\ \Rightarrow {h_1} = 2{h_2}\\ \Rightarrow {h_2} = \frac{{{h_1}}}{3} = 5\;{\rm{cm}}\end{array}\)

\( \Rightarrow \) pitong dịch sang trái 10 cm.

Đáp án đúng là B

Phương pháp giải

Sử dụng tương giao đồ thị

Lời giải

Xét hàm số \(y = f\left( {{x^2} - 3x + m} \right)\) có

\({y^\prime } = (2x - 3).{f^\prime }\left( {{x^2} - 3x + m} \right)\)

\({y^\prime } = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{2x - 3 = 0}\\{{f^\prime }\left( {{x^2} - 3x + m} \right) = 0}\end{array}} \right.\)

Để hàm số \(y = f\left( {{x^2} - 3x + m} \right)\) có nhiều cực trị nhất thì phương trình \({f^\prime }\left( {{x^2} - 3x + m} \right) = 0\) có nhiều nghiệm bội lẻ khác \(\frac{3}{2}\) nhất.

Xét phương trình: \({f^\prime }\left( {{x^2} - 3x + m} \right) = 0 \Leftrightarrow \left( {{x^2} - 3x + m + 3} \right)\left( {{x^2} - 3x + m - 4} \right) = 0\)

\( \Rightarrow \left[ {\begin{array}{*{20}{l}}{{x^2} - 3x = - m - 3}\\{{x^2} - 3x = 4 - m}\end{array}} \right.\)

Xét hàm số : \(h(x) = {x^2} - 3x\)

\({h^\prime }(x) = 2x - 3,{h^\prime } = 0 \Rightarrow x = \frac{3}{2}\)

Bảng biến thiên hàm số \(h(x) = {x^2} - 3x\)

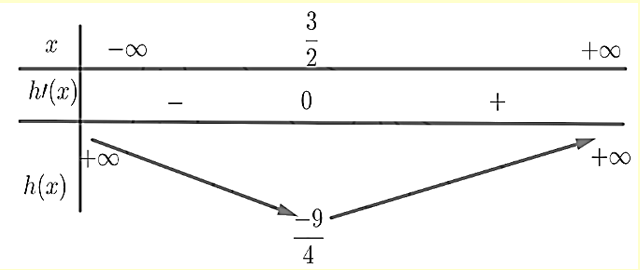
Để \({f^\prime }\left( {{x^2} - 3x + m} \right) = 0 \Leftrightarrow \left( {{x^2} - 3x + m + 3} \right)\left( {{x^2} - 3x + m - 4} \right) = 0\) có nhiều nghiệm bội lẻ nhất \( \Rightarrow \left[ {\begin{array}{*{20}{l}}{{x^2} - 3x = - m - 3}\\{{x^2} - 3x = 4 - m}\end{array}} \right.\) có nhiều nghiệm bội lẻ nhất

Số nghiệm của hai phương trình này là số giao điểm của đồ thị hàm số \(h(x) = {x^2} - 3x\) và các đường thẳng \(y = - m - 3\) và \(y = 4 - m\)

Dựa vào bảng biến thiên của hàm số \(h(x) = {x^2} - 3x \Rightarrow \left[ {\begin{array}{*{20}{l}}{ - m - 3 > \frac{{ - 9}}{4}}\\{4 - m > \frac{{ - 9}}{4}}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m < \frac{{ - 3}}{4}}\\{m < \frac{{25}}{4}}\end{array}} \right.} \right.\)

Mà \(m \in [ - 10;5]\), kết hợp các điều kiện \( \Rightarrow m \in \left( {\frac{{ - 3}}{4};5} \right],m \in \mathbb{Z} \Rightarrow m \in \{ 0;1;2;3;4;5\} \)

Vậy tổng các giá trị nguyên của \(m\) thỏa mãn yêu cầu bài toán là: 15