Đọc đoạn trích sau và trả lời câu hỏi:

     Các nhà khoa học thuộc Đại học Harvard (Mỹ), với trưởng nhóm là nhà địa chất Nadja Drabon, đã khám phá ra bằng chứng về cú va chạm này thông qua những lớp đá lâu đời tại Vành đai đá xanh Barberton (Barberton Greenstone Belt) - một khu vực ở Đông Bắc Nam Phi. Những dấu hiệu địa hóa và hóa thạch vi khuẩn biển được bảo tồn trong đá cho thấy thay vì bị hủy diệt, sự sống không chỉ hồi phục mà còn phát triển mạnh mẽ sau cú va chạm khủng khiếp này. Theo nghiên cứu, thiên thạch va chạm với Trái đất khoảng 3,26 tỉ năm trước có đường kính ước tính từ 37-58km, lớn hơn nhiều so với thiên thạch đã khiến loài khủng long tuyệt chủng. Loại thiên thạch có tên khoa học là "carbonaceous chondrite" này chứa nhiều các-bon và phốt pho - những yếu tố quan trọng cho sự sống. Năng lượng từ cú va chạm cực mạnh đã khiến thiên thạch bốc hơi hoàn toàn cùng với lớp trầm tích và đá mà nó va chạm vào, tạo ra một đám mây bụi và hơi đá bao phủ toàn bộ Trái Đất, biến bầu trời thành màu đen chỉ trong vài giờ. Không chỉ vậy, sóng thần khổng lồ do va chạm tạo ra đã quét sạch đáy biển và nhấn chìm các bờ biển khắp thế giới. Nhiệt độ bề mặt đại dương tăng cao đến mức lớp nước trên cùng bắt đầu sôi, tạo nên một khung cảnh khủng khiếp của sự hủy diệt. Dù những hình ảnh về sự tàn phá gần như toàn diện ấy có vẻ đáng sợ, các nhà khoa học tin rằng cú va chạm này đã đóng vai trò như một “quả bom phân bón khổng lồ” cho sự sống nguyên thủy. Sau khi bụi lắng xuống và nhiệt độ trở lại bình thường, thiên thạch đã mang đến cho Trái đất một lượng lớn phốt pho - chất dinh dưỡng cực kỳ quan trọng cho vi khuẩn. Đồng thời, sóng thần đã làm trộn lẫn các lớp nước sâu giàu sắt với các vùng nước nông, tạo ra một môi trường hoàn hảo cho các vi khuẩn và sinh vật đơn bào cổ đại phát triển mạnh mẽ.

(TTXVN, Một thiên thạch khổng lồ từng lao xuống Trái đất, lớn gấp 200 lần thiên thạch xóa sổ khủng long, Theo Tuoitre.vn, ngày 22/10/2024)

Nội dung nào KHÔNG được nhắc đến trong đoạn trích trên?

Đáp án đúng là D

Phương pháp giải

Sử dụng công thức tính tính thể tích: V = hS

Xác định các thông số trạng thái.

Áp dụng công thức định luật Boyle.

Lời giải

Xét trạng thái 1: \(\left\{ {\begin{array}{*{20}{l}}{{p_1}}\\{{V_1} = {h_1}S}\end{array}} \right.\)

Xét trạng thái 2: \(\left\{ {\begin{array}{*{20}{l}}{{p_2} = 3{p_1}}\\{{V_2} = {h_2}S}\end{array}} \right.\)

Quá trình đẳng nhiệt diễn ra nên ta có: \({p_1}{V_1} = {p_2}{V_2}\)

\(\begin{array}{l} \Rightarrow {p_1}{h_1}S = 3{p_1}{h_2}S\\ \Rightarrow {h_1} = 2{h_2}\\ \Rightarrow {h_2} = \frac{{{h_1}}}{3} = 5\;{\rm{cm}}\end{array}\)

\( \Rightarrow \) pitong dịch sang trái 10 cm.

Đáp án đúng là B

Phương pháp giải

Sử dụng tương giao đồ thị

Lời giải

Xét hàm số \(y = f\left( {{x^2} - 3x + m} \right)\) có

\({y^\prime } = (2x - 3).{f^\prime }\left( {{x^2} - 3x + m} \right)\)

\({y^\prime } = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{2x - 3 = 0}\\{{f^\prime }\left( {{x^2} - 3x + m} \right) = 0}\end{array}} \right.\)

Để hàm số \(y = f\left( {{x^2} - 3x + m} \right)\) có nhiều cực trị nhất thì phương trình \({f^\prime }\left( {{x^2} - 3x + m} \right) = 0\) có nhiều nghiệm bội lẻ khác \(\frac{3}{2}\) nhất.

Xét phương trình: \({f^\prime }\left( {{x^2} - 3x + m} \right) = 0 \Leftrightarrow \left( {{x^2} - 3x + m + 3} \right)\left( {{x^2} - 3x + m - 4} \right) = 0\)

\( \Rightarrow \left[ {\begin{array}{*{20}{l}}{{x^2} - 3x = - m - 3}\\{{x^2} - 3x = 4 - m}\end{array}} \right.\)

Xét hàm số : \(h(x) = {x^2} - 3x\)

\({h^\prime }(x) = 2x - 3,{h^\prime } = 0 \Rightarrow x = \frac{3}{2}\)

Bảng biến thiên hàm số \(h(x) = {x^2} - 3x\)

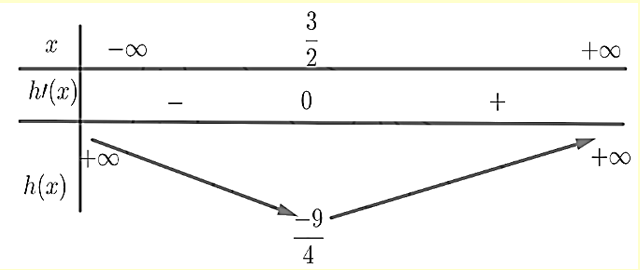
Để \({f^\prime }\left( {{x^2} - 3x + m} \right) = 0 \Leftrightarrow \left( {{x^2} - 3x + m + 3} \right)\left( {{x^2} - 3x + m - 4} \right) = 0\) có nhiều nghiệm bội lẻ nhất \( \Rightarrow \left[ {\begin{array}{*{20}{l}}{{x^2} - 3x = - m - 3}\\{{x^2} - 3x = 4 - m}\end{array}} \right.\) có nhiều nghiệm bội lẻ nhất

Số nghiệm của hai phương trình này là số giao điểm của đồ thị hàm số \(h(x) = {x^2} - 3x\) và các đường thẳng \(y = - m - 3\) và \(y = 4 - m\)

Dựa vào bảng biến thiên của hàm số \(h(x) = {x^2} - 3x \Rightarrow \left[ {\begin{array}{*{20}{l}}{ - m - 3 > \frac{{ - 9}}{4}}\\{4 - m > \frac{{ - 9}}{4}}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m < \frac{{ - 3}}{4}}\\{m < \frac{{25}}{4}}\end{array}} \right.} \right.\)

Mà \(m \in [ - 10;5]\), kết hợp các điều kiện \( \Rightarrow m \in \left( {\frac{{ - 3}}{4};5} \right],m \in \mathbb{Z} \Rightarrow m \in \{ 0;1;2;3;4;5\} \)

Vậy tổng các giá trị nguyên của \(m\) thỏa mãn yêu cầu bài toán là: 15