Hai nguồn kết hợp A, B cùng pha, cùng biên độ, cách nhau 40 cm. Khoảng cách giữa hai điểm dao động với biên độ cực đại gần nhau nhất trên đoạn AB là 0,8 cm. Điểm M thuộc miền giao thoa cách nguồn A một đoạn 25cm và cách nguồn B một đoạn 22cm. Dịch chuyển nguồn B từ từ dọc theo phương AB ra xa nguồn B đoạn 10 cm thì số lần điểm M chuyển thành điểm dao động với biên độ cực đại là:
Hai nguồn kết hợp A, B cùng pha, cùng biên độ, cách nhau 40 cm. Khoảng cách giữa hai điểm dao động với biên độ cực đại gần nhau nhất trên đoạn AB là 0,8 cm. Điểm M thuộc miền giao thoa cách nguồn A một đoạn 25cm và cách nguồn B một đoạn 22cm. Dịch chuyển nguồn B từ từ dọc theo phương AB ra xa nguồn B đoạn 10 cm thì số lần điểm M chuyển thành điểm dao động với biên độ cực đại là:
A. 6 lần
B. 8 lần
C. 7 lần
D. 5 lần
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là D
Phương pháp giải
Xác định bước sóng của sóng.
Sử dụng điều kiện để phần tử dao động cực đại: \({d_1} - {d_2} = k\lambda \)
Lời giải
Khoảng cách giữa hai điểm dao động với biên độ cực đại gần nhau nhất trên đoạn AB là 0,8 cm
\( \Rightarrow \frac{\lambda }{2} = 0,8 \Rightarrow \lambda = 1,6(\;{\rm{cm}})\)
Ta có hình ảnh minh họa:
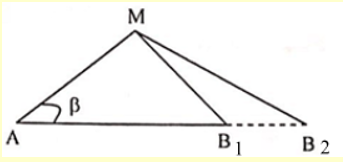
Từ hình ta có:
\(\cos \beta = \frac{{A{M^2} + {{\left( {A{B_1}} \right)}^2} - {{\left( {M{B_1}} \right)}^2}}}{{2AM.A{B_1}}} = \frac{{{{25}^2} + {{40}^2} - {{22}^2}}}{{2.25.40}} = 0,8705\)
Xét trong tam giác \(AM{B_2}\) ta có:
\(M{B_2} = \sqrt {A{M^2} + {{\left( {A{B_2}} \right)}^2} - 2AM.A{B_2}.\cos \beta } = \sqrt {{{25}^2} + {{50}^5} - 2.25.50.0,8705} = 30,8\,\,({\rm{cm}})\)
Điểm \(M\) thuộc cực đại khi: \({d_{1M}} - {d_{2M}} = k\lambda = 1,6k\)
Mặt khác:
\(\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}{\Delta {d_{M - 1}} = AM - M{B_1} = 25 - 22 = 3\;{\rm{cm}}}\\{\Delta {d_{M - 2}} = AM - M{B_2} = 25 - 30,8 = - 5,8\;{\rm{cm}}}\end{array}} \right.\\ \Rightarrow - 5,8 \le 1,6k \le 3\\ \Rightarrow - 3,6 \le k \le 1,8\\ \Rightarrow k = - 3; - 2; - 1;0;1\end{array}\)
Vậy có 5 giá trị của k thỏa mãn hay điểm M sẽ chuyển thành điểm dao động cực đại 5 lần.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. sang phải 5cm.
B. sang trái 5cm.
C. sang phải 10cm.
D. sang trái 10cm.
Lời giải
Đáp án đúng là D
Phương pháp giải
Sử dụng công thức tính tính thể tích: V = hS
Xác định các thông số trạng thái.
Áp dụng công thức định luật Boyle.
Lời giải
Xét trạng thái 1: \(\left\{ {\begin{array}{*{20}{l}}{{p_1}}\\{{V_1} = {h_1}S}\end{array}} \right.\)
Xét trạng thái 2: \(\left\{ {\begin{array}{*{20}{l}}{{p_2} = 3{p_1}}\\{{V_2} = {h_2}S}\end{array}} \right.\)
Quá trình đẳng nhiệt diễn ra nên ta có: \({p_1}{V_1} = {p_2}{V_2}\)
\(\begin{array}{l} \Rightarrow {p_1}{h_1}S = 3{p_1}{h_2}S\\ \Rightarrow {h_1} = 2{h_2}\\ \Rightarrow {h_2} = \frac{{{h_1}}}{3} = 5\;{\rm{cm}}\end{array}\)
\( \Rightarrow \) pitong dịch sang trái 10 cm.
Câu 2
A. Nhiệt độ trung bình năm giảm dần từ Nam ra Bắc do nước ta lãnh thổ nước ta hẹp ngang, nhiều đồi núi.
B. Biên độ nhiệt năm giảm dần từ Nam ra Bắc do miền Nam không chịu ảnh hưởng của gió mùa Đông Bắc.
C. Bãi Cháy có biên độ nhiệt trung bình năm cao do vị trí địa lí và ảnh hưởng của gió mùa mùa đông.
D. Chênh lệch nhiệt độ trung bình năm giữa Cà Mau và Đà Nẵng là 1,4°C do đều nằm ở vùng khí hậu phía Nam.
Lời giải
Đáp án đúng là D
Phương pháp giải
Nhận xét bảng số liệu, kết hợp với phần Thiên nhiên nhệt đới ẩm gió mùa.
Lời giải
- Chênh lệch nhiệt độ trung bình năm giữa Cà Mau và Đà Nẵng là 1,4°C do đều nằm ở vùng khí hậu phía Nam là nhận xét đúng. Vùng khí hậu phía Bắc và vùng khí hậu Nam được ngăn cách bởi dãy Bạch Mã. Gió mùa Đông Bắc bị chặn lại tại dãy Bạch Mã nên vùng khí hậu phía Nam không chịu ảnh hưởng của gió mùa Đông Bắc => Cà Mau và Đà Nẵng thuộc vùng khí hậu phía Nam, quanh năm nhiệt độ cao => ít có sự chênh lệch nhiệt độ trung bình năm giữa hai địa điểm này.
- A sai vì nhiệt độ trung bình năm giảm dần từ Nam ra Bắc do càng ra Bắc góc nhập xạ càng nhỏ, miền Bắc chịu ảnh hưởng của gió mùa Đông Bắc,…
- B sai vì biên độ nhiệt năm tăng dần từ Nam ra Bắc.
- C sai vì nhiệt độ trung bình năm của Bãi Cháy không cao, so với Đà Nẵng, Cà Mau là thấp hơn.
Câu 3
A. Hiện tượng đồng âm
B. Hiện tượng trái nghĩa
C. Hiện tượng đồng nghĩa
D. Hiện tượng đa nghĩa
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Lào cao hơn Cam-pu-chia và thấp hơn In-đô-nê-xi-a.
B. In-đô-nê-xi-a cao hơn Cam-pu-chia và thấp hơn Lào.
C. Cam-pu-chia cao hơn In-đô-nê-xi-a và cao hơn Lào.
D. Cam-pu-chia cao hơn In-đô-nê-xi-a và thấp hơn Lào.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. (I), (II), (III)
B. (II), (III), (IV)
C. (I), (III), (IV)
D. (I), (II), (IV)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập