Choose A, B, C or D to answer the question.

You are in a study group where some classmates are already working on a challenging homework assignment. You haven’t started yet and feel a bit nervous to ask for help, but you want to join them. What can you say to participate in the group homework session?

 

Đáp án đúng là D

Phương pháp giải

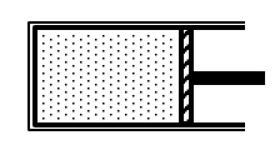
Sử dụng công thức tính tính thể tích: V = hS

Xác định các thông số trạng thái.

Áp dụng công thức định luật Boyle.

Lời giải

Xét trạng thái 1: \(\left\{ {\begin{array}{*{20}{l}}{{p_1}}\\{{V_1} = {h_1}S}\end{array}} \right.\)

Xét trạng thái 2: \(\left\{ {\begin{array}{*{20}{l}}{{p_2} = 3{p_1}}\\{{V_2} = {h_2}S}\end{array}} \right.\)

Quá trình đẳng nhiệt diễn ra nên ta có: \({p_1}{V_1} = {p_2}{V_2}\)

\(\begin{array}{l} \Rightarrow {p_1}{h_1}S = 3{p_1}{h_2}S\\ \Rightarrow {h_1} = 2{h_2}\\ \Rightarrow {h_2} = \frac{{{h_1}}}{3} = 5\;{\rm{cm}}\end{array}\)

\( \Rightarrow \) pitong dịch sang trái 10 cm.

Đáp án đúng là C

Phương pháp giải

Xác suất có điều kiện

Lời giải

\(\Omega = \{ GG;GT;TG,TT\} \)

Số phần tử không gian mẫu: \({n_\Omega } = 4\)

Gọi \(A\) là biến cố : "2 người con đều là gái"

Gọi \(B\) là biến cố : "Có ít nhất một người con là gái"

Số phần tử của biến cố \(A\) là \({n_A} = 1\)

Số phần tử của biến cố \(B\) là \({n_B} = 3\)

\( \Rightarrow n(A \cap B) = 1\)

\(P(A\mid B) = \frac{{n(A \cap B)}}{{n(B)}} = \frac{1}{3}\)