Choose A, B, C or D to answer the question.
Kate, the manager, is asking David, her assistant, about his preparation for an upcoming business trip. What would be the best response for David in this situation?
Kate: Are you ready for the business trip next week?
David: ________
Choose A, B, C or D to answer the question.
Kate, the manager, is asking David, her assistant, about his preparation for an upcoming business trip. What would be the best response for David in this situation?
Kate: Are you ready for the business trip next week?
David: ________
A. I’ve almost got everything set. Just finalizing the travel itinerary.
B. I’m not sure. Have you already spoken to the client about this?
C. Business trips are always exciting. But I'm not prepared yet.
D. Don’t worry! I’m sure the trip will be a success, no matter what.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là A
Phương pháp giải
Câu hỏi tình huống
Lời giải
Kate, người quản lý, đang hỏi David, trợ lý của cô, về việc chuẩn bị cho chuyến công tác sắp tới. Câu trả lời tốt nhất cho David trong tình huống này là gì?
Kate: Anh đã sẵn sàng cho chuyến công tác vào tuần tới chưa?
David: ________
A. Tôi đã chuẩn bị gần xong mọi thứ. Chỉ đang hoàn thiện hành trình du lịch.
B. Tôi không chắc. Anh đã nói chuyện với khách hàng về việc này chưa?
C. Các chuyến công tác luôn thú vị. Nhưng tôi vẫn chưa chuẩn bị.
D. Đừng lo! Tôi chắc chắn chuyến đi sẽ thành công, bất kể thế nào.
Đáp án A cho thấy David đã chuẩn bị tốt cho chuyến công tác sắp tới đồng thời cũng cung cấp thông tin cập nhật cụ thể về những gì anh ấy đang làm. Các lựa chọn khác thể hiện sự không chắc chắn, thiếu chuẩn bị hoặc chuyển hướng khỏi việc giải quyết trực tiếp câu hỏi, điều này có thể làm Kate lo ngại về sự sẵn sàng của David.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. sang phải 5cm.
B. sang trái 5cm.
C. sang phải 10cm.
D. sang trái 10cm.
Lời giải
Đáp án đúng là D
Phương pháp giải
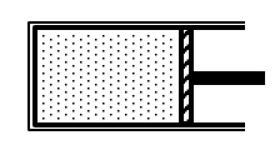
Sử dụng công thức tính tính thể tích: V = hS
Xác định các thông số trạng thái.
Áp dụng công thức định luật Boyle.
Lời giải
Xét trạng thái 1: \(\left\{ {\begin{array}{*{20}{l}}{{p_1}}\\{{V_1} = {h_1}S}\end{array}} \right.\)
Xét trạng thái 2: \(\left\{ {\begin{array}{*{20}{l}}{{p_2} = 3{p_1}}\\{{V_2} = {h_2}S}\end{array}} \right.\)
Quá trình đẳng nhiệt diễn ra nên ta có: \({p_1}{V_1} = {p_2}{V_2}\)
\(\begin{array}{l} \Rightarrow {p_1}{h_1}S = 3{p_1}{h_2}S\\ \Rightarrow {h_1} = 2{h_2}\\ \Rightarrow {h_2} = \frac{{{h_1}}}{3} = 5\;{\rm{cm}}\end{array}\)
\( \Rightarrow \) pitong dịch sang trái 10 cm.
Câu 2
A. Hiện tượng đồng âm
B. Hiện tượng trái nghĩa
C. Hiện tượng đồng nghĩa
D. Hiện tượng đa nghĩa
Lời giải
Đáp án đúng là A
Phương pháp giải
Căn cứ vào kiến thức về từ đồng âm, từ nhiều nghĩa.
Nội dung/ Thông điệp
Lời giải
- Từ “đường” trong bài thơ trên là con đường để đi lại, con đường giao thông.
- Từ “đường” trong cụm từ “ngọt như đường” có nghĩa là đường thực phẩm, đường dùng trong nấu ăn, pha chế, có vị ngọt.
- Hai từ “đường” khác biệt hoàn toàn về nghĩa, chỉ có âm giống nhau, đây là hiện tượng từ đồng âm.
Câu 3
A. Nhiệt độ trung bình năm giảm dần từ Nam ra Bắc do nước ta lãnh thổ nước ta hẹp ngang, nhiều đồi núi.
B. Biên độ nhiệt năm giảm dần từ Nam ra Bắc do miền Nam không chịu ảnh hưởng của gió mùa Đông Bắc.
C. Bãi Cháy có biên độ nhiệt trung bình năm cao do vị trí địa lí và ảnh hưởng của gió mùa mùa đông.
D. Chênh lệch nhiệt độ trung bình năm giữa Cà Mau và Đà Nẵng là 1,4°C do đều nằm ở vùng khí hậu phía Nam.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Lào cao hơn Cam-pu-chia và thấp hơn In-đô-nê-xi-a.
B. In-đô-nê-xi-a cao hơn Cam-pu-chia và thấp hơn Lào.
C. Cam-pu-chia cao hơn In-đô-nê-xi-a và cao hơn Lào.
D. Cam-pu-chia cao hơn In-đô-nê-xi-a và thấp hơn Lào.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. (I), (II), (III)
B. (II), (III), (IV)
C. (I), (III), (IV)
D. (I), (II), (IV)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập