Cho tứ diện đều \[ABCD\] có cạnh bằng \(2\sqrt 2 \). Gọi \(M\), \(N\) lần lượt là trọng tâm của các tam giác\(ABD\),\(ABC\) và \(E\) là điểm đối xứng với \(B\) qua điểm \(D\). Mặt phẳng \(\left( {MNE} \right)\) chia khối tứ diện \[ABCD\] thành hai khối đa diện, trong đó khối đa diện chứa đỉnh \(A\) có thể tích \(V\). Tính \(V\).
Câu hỏi trong đề: Bộ 14 đề thi giữa kì 2 Toán 11 cấu trúc mới !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án:
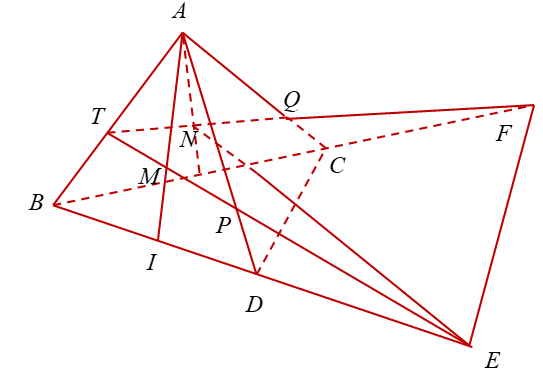
Thể tích khối tứ diện đều cạnh \(2\sqrt 2 \) là: \(\frac{8}{3}\).
Gọi \(P = ME \cap AD\); \(T = ME \cap AB\). Trong mặt phẳng \(\left( {ABC} \right)\) đường thẳng \(TN\) cắt \(AC\),\(BC\) lần lượt tại \(Q\),\(F\). Khi đó mặt phẳng \(\left( {MNE} \right)\) chia khối tứ diện đã cho phần chứa đỉnh \(A\) là tứ diện \(ATPQ\).
Gọi \(I\) là trung điểm \(BD\). Xét \(\Delta AID\) ta có: \(\frac{{ED}}{{EI}}.\frac{{MI}}{{MA}}.\frac{{PA}}{{PD}} = 1\) (định lý Menelaus)\( \Rightarrow \frac{{PA}}{{PD}} = 3\).
Tương tự ta có: \(\frac{{QA}}{{QC}} = 3\)
Xét \(\Delta AIB\) ta có: \(\frac{{EI}}{{EB}}.\frac{{TB}}{{TA}}.\frac{{MA}}{{MI}} = 1\)\( \Leftrightarrow \frac{{TB}}{{TA}} = \frac{2}{3}\).
Mặt khác ta có: \(\frac{{{V_{ATPQ}}}}{{{V_{ABCD}}}} = \frac{{AT}}{{AB}}.\frac{{AP}}{{AD}}.\frac{{AQ}}{{AC}} = \frac{3}{5}.\frac{3}{4}.\frac{3}{4} = \frac{{27}}{{80}}\) \( \Rightarrow {V_{ATPQ}} = \frac{{27}}{{80}}.\frac{{{{\left( {2\sqrt 2 } \right)}^3}\sqrt 2 }}{{12}} = \frac{9}{{10}} = 0,9\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi cuối kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án:
Gọi I là trung điểm BC. Suy ra : \(SI \bot BC\) và \(HI \bot BC\)
\( \Rightarrow \) Góc giữa hai mặt phẳng \[\left( {SBC} \right)\]và \[\left( {ABCD} \right)\]là \(\widehat {SIH}\)
Ta có: \(HI = \frac{{AB}}{2} = 131\) (m)
Xét \({\rm{\Delta SHI}}\) vuông tại H ta có: \(\tan \widehat {SIH} = \frac{{SH}}{{HI}} = \frac{{\sqrt {18578} }}{{131}} \Rightarrow \widehat {SIH} \approx {46^0}\)
Vậy góc giữa mặt bên và mặt đáy của kim tự tháp là khoảng \({46^0}\).
Câu 2
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Chọn A
Thay các dữ kiện ta có phương trình \(300 = 100.{e^{5r}} \Rightarrow r = \frac{{\ln 3}}{5}.\)
Để số lượng vi khuẩn tăng \(10\) lần (tức \(1000\) con), ta có \(1000 = 100.{e^{\frac{{\ln 3}}{5}t}} \Rightarrow t = \frac{5}{{\log 3}}.\)
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập