Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi cạnh \(2\sqrt 3 \), \(\widehat {BAD} = 60^\circ \), gọi I là giao điểm \(AC\) và \(BD\). Hình chiếu vuông góc của S lên mặt phẳng \((ABCD)\) là \(H\) sao cho \(H\) là trung điểm của \(BI\). Góc giữa \(SC\) và \((ABCD)\) bằng \(45^\circ \). Thể tích \(V\) của khối chóp \(S.ABCD\)là \(\sqrt a \). Tìm \(a\)?
Quảng cáo
Trả lời:
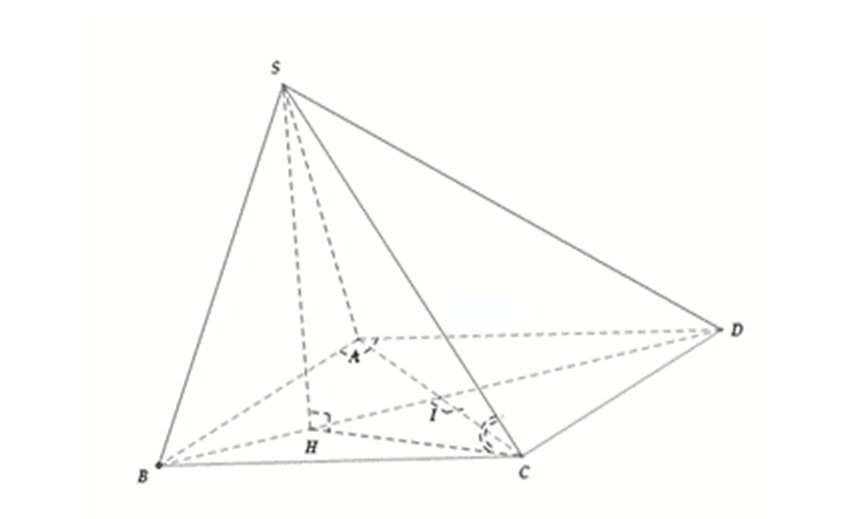
Tam giác \(ABD\) đều cạnh \(2\sqrt 3 \)\( \Rightarrow \) \(BD = 2\sqrt 3 \Rightarrow IH = \frac{{\sqrt 3 }}{2}\)
Áp dụng định lí cosin cho tam giác \(ABC:\,\,AC = \sqrt {{{\left( {2\sqrt 3 } \right)}^2} + {{\left( {2\sqrt 3 } \right)}^2} - 2.2\sqrt 3 .2\sqrt 3 .c{\rm{os120}}^\circ } = 6 \Rightarrow IC = 3\)
Xét tam giác \(IHC\) vuông tại \[I\]: \(HC = \sqrt {I{H^2} + I{C^2}} = \sqrt {{{\left( {\frac{{\sqrt 3 }}{2}} \right)}^2} + {3^2}} = \frac{{\sqrt {39} }}{2}\)
Do tam giác \(SHC\) vuông tại \(H\), có \(\widehat {SCH} = \left( {SC,\,\left( {ABCD} \right)} \right) = 45^\circ \)nên tam giác \(SHC\) vuông cân tại \(H\). Suy ra: \(HC = SH = \frac{{\sqrt {39} }}{2}\)
Thể tích khối chóp \(S.ABCD\): \[{V_{S.ABCD}} = \frac{1}{3}.\frac{1}{2}.AC.BD.SH = \frac{1}{6}.6.2\sqrt 3 .\frac{{\sqrt {39} }}{2} = \sqrt {117} \]
Vậy \(a = 117\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
a) Đúng
b) Đúng
\[N = 95,93.{(1 + 1,33\% )^7} \approx 105,23\]triệu người
c) Sai
Số dân tăng từ năm 2018 đến năm 2027: \[N = 95,93.{\left( {1 + 1,33} \right)^9} - 95,93 \approx 12,11\] triệu người.
d) Sai
\[108,04 = 95,93.{\left( {1 + 1,33} \right)^n} \Rightarrow n = 9 = m\]
\[P = 2{\log _3}9 + 1 = 5\]
Lời giải
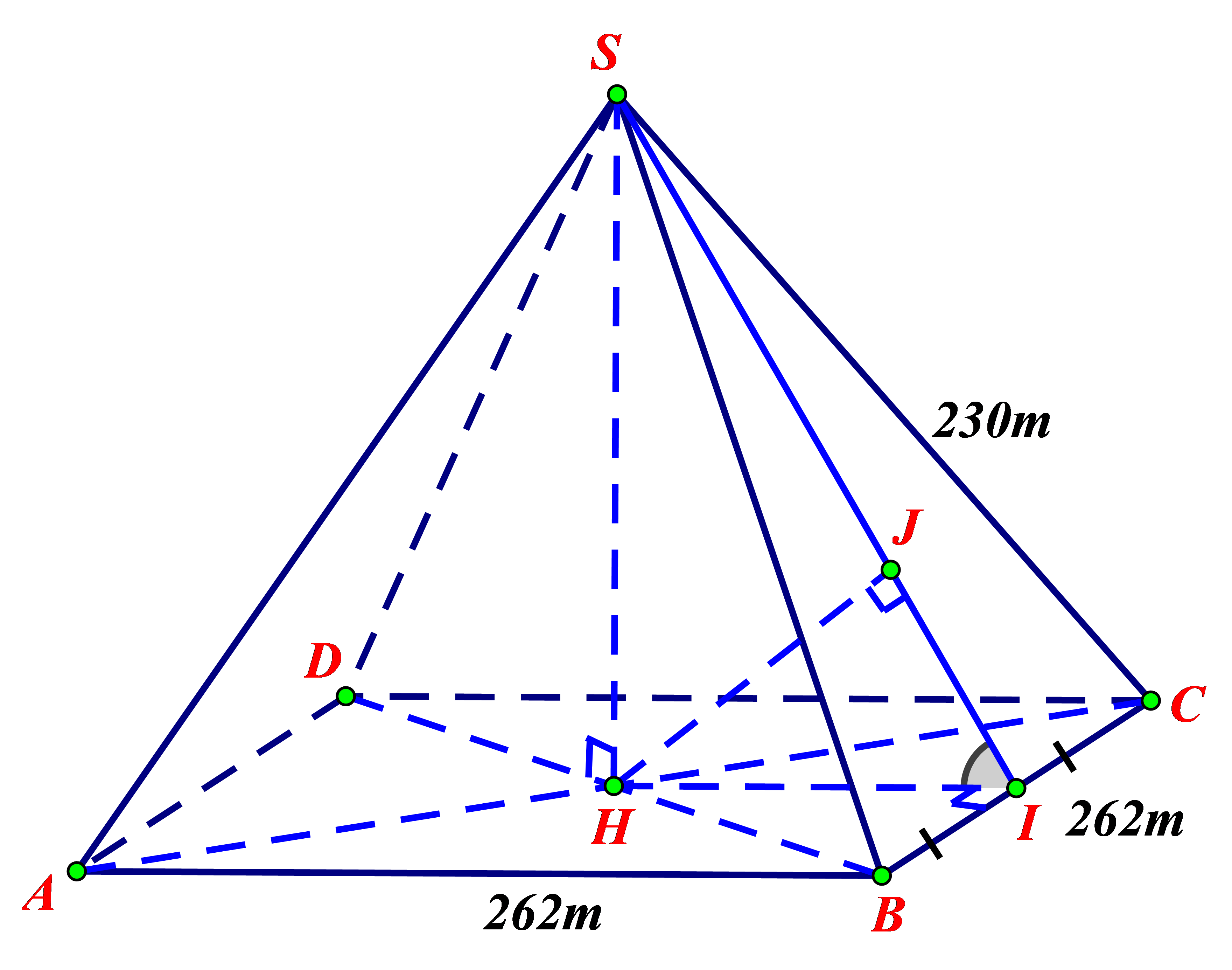
Giả sử các cạnh và đỉnh của kim tự tháp như hình vẽ. Vì S.ABCD hình chóp tứ giác đều nên \[SH \bot \left( {ABCD} \right)\;\](\(H = AC \cap BD\) )
Xét \({\rm{\Delta ABC}}\) vuông tại A, ta có: \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{262}^2} + {{262}^2}} = 262\sqrt 2 \) (m).
\( \Rightarrow HC = \frac{{AC}}{2} = 131\sqrt 2 \) (m).
Xét \({\rm{\Delta SHC}}\) vuông tại H, ta có: \(SH = \sqrt {S{C^2} - H{C^2}} = \sqrt {{{230}^2} - {{(131\sqrt 2 )}^2}} = \sqrt {18578} \)(m).
Kẻ HJ vuông góc với SI, vì \(BC \bot HI,BC \bot SH \Rightarrow BC \bot HJ.\)
\(HJ \bot SI,HJ \bot BC \Rightarrow HJ \bot \left( {SBC} \right) \Rightarrow HJ = d\left( {H,\left( {SBC} \right)} \right).\)
Do đó \[HJ\]là đoạn đường ngắn nhất từ mặt bên đến kho báu.
Trong tam giác \[SHI\]vuông tại \[H\], ta có: \(HJ = \frac{{SH.SI}}{{\sqrt {S{H^2} + S{I^2}} }} \approx 94\left( m \right).\)
Vậy độ dài ngắn nhất cần tìm xấp xỉ \(94\,\,\left( m \right).\)
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
a) SO vuông góc (ABCD)
b) CD vuông góc (SBD)
c) AB vuông góc (SAC)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.