Một ngôi tháp nghiêng về phía Tây một góc α so với phương ngang của mặt đất. Vào lúc 10 giờ sáng, khi góc nâng của tia sáng mặt trời so với mặt đất có số đo là \(60^\circ \) thì bóng của tháp trải trên mặt đất dài 37,5 m. Vào lúc 16 giờ chiếu, khi góc nâng của tia nắng mặt trời so với mặt đất có số đo là \(45^\circ \) thì bóng của tháp trải trên mặt đất là 51,9 m.
a) Tính chiều dài thân tháp nghiêng trên.
b) Tìm số đo góc α.
Câu hỏi trong đề: Bài tập ôn tập Toán 10 Kết nối tri thức Chương 3 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
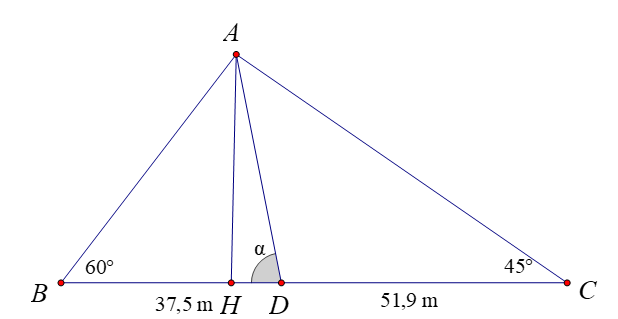
Ta có \(\widehat {BAC} = 180^\circ - 60^\circ - 45^\circ = 75^\circ \); \(BC = 37,5 + 51,9 = 89,4\).
Áp dụng định lí sin cho tam giác \(ABC\), ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}} \Rightarrow AB = \frac{{BC\sin C}}{{\sin A}} = \frac{{89,4 \cdot \sin 45^\circ }}{{\sin 75^\circ }} \approx 65,45\) (m).
Áp dụng định lí cô sin cho tam giác \(ABD\), ta có
\(A{D^2} = A{B^2} + B{D^2} - 2AB \cdot BD \cdot \cos \widehat {ABC} = 65,{45^2} + 37,{5^2} - 2 \cdot 65,45 \cdot 37,5 \cdot \cos 60^\circ \).
Suy ra \(AD \approx 56,88\) m.
Vậy chiều cao thân tháp là 56,88 m.
b) Xét \(\Delta AHB\), có \[AH = AB \cdot \sin B = 65,45 \cdot \sin 60^\circ \approx 56,68\] (m).
Khi đó \(\sin \alpha = \frac{{AH}}{{AD}} = 0,9965 \Rightarrow \alpha \approx 85^\circ 11'\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi cuối kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án:
Xét \(\Delta ACH\) có \(AH = \frac{{CH}}{{\tan 45^\circ }}\).
Xét \(\Delta BCH\) có \(BH = \frac{{CH}}{{\tan 35^\circ }}\).
Có \(AH + BH = 105\) nên \(\frac{{CH}}{{\tan 45^\circ }} + \frac{{CH}}{{\tan 35^\circ }} = 105\)\( \Leftrightarrow CH = 105:\left( {\frac{1}{{\tan 45^\circ }} + \frac{1}{{\tan 35^\circ }}} \right) \approx 43,2\)(m).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án:
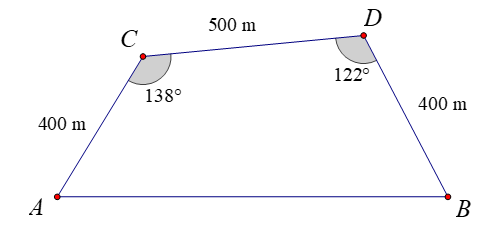
Áp dụng định lí cô sin cho tam giác \(BCD\), có
\(B{C^2} = C{D^2} + B{D^2} - 2CD \cdot DB \cdot \cos D = {500^2} + {400^2} - 2 \cdot 500 \cdot 400 \cdot \cos 122^\circ \Rightarrow BC \approx 789\)(m).
Áp dụng định lí sin cho tam giác \(BCD\), có:
\(\frac{{BC}}{{\sin D}} = \frac{{BD}}{{\sin C}} \Rightarrow \sin C = \frac{{BD \cdot \sin D}}{{BC}} = \frac{{400 \cdot \sin 122^\circ }}{{789}} \Rightarrow \widehat C \approx 25,5^\circ \).
Suy ra \(\widehat {ACB} = 138^\circ - 25,5^\circ = 112,5^\circ \).
Áp dụng định lí cô sin cho tam giác \(ABC\), có
\(A{B^2} = A{C^2} + B{C^2} - 2AC \cdot BC \cdot \cos C = {400^2} + {789^2} - 2 \cdot 400 \cdot 789 \cdot \cos 112,5^\circ \Rightarrow AB \approx 1012\) (m).
Câu 3
a) Giá trị \(\sin \alpha \cdot \cos \alpha < 0\).
b) Có \(\sin \alpha = \frac{{2\sqrt 2 }}{3}\).
c) Có \(\tan \alpha = \frac{{\sqrt 2 }}{4}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
a) \(AB \approx 7,20\)(kết quả làm tròn đến hàng phần trăm).
b) Góc \(A\) là góc tù.
c) Bán kính đường tròn nội tiếp tam giác \(ABC\) xấp xỉ bằng 1,96 (kết quả làm tròn đến hàng phần trăm).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
a) \(p = 14\).
b) \(S = 13\sqrt 5 \).
c) \(R = \frac{{7\sqrt 5 }}{{10}}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập