Trong không gian Oxyz, cho điểm \(A(1;1;1)\), mặt phẳng \((P):x + y + z - 3 = 0\) và đường thẳng \(d:\frac{{x - 2}}{1} = \frac{y}{2} = \frac{z}{{ - 1}}\). Xét đường thẳng \(\Delta \) qua \(A\), nằm trong \((P)\) và cách đường thẳng \(d\) một khoảng cách lớn nhất. Đường thẳng \(\Delta \) đi qua điểm nào dưới đây?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là B
Phương pháp giải
Xác định phương trình đường thẳng \(\Delta \)
Lời giải
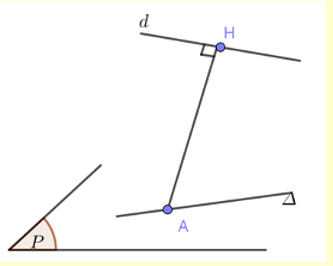
Gọi \(H(x;y;z)\) là hình chiếu vuông góc của \(A\) trên \(d\).
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{H \in d}\\{\overrightarrow {AH} .\overrightarrow {{u_d}} = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\frac{{x - 2}}{1} = \frac{y}{2} = \frac{z}{{ - 1}}}\\{1(x - 1) + 2(y - 1) - 1(z - 1) = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 2}\\{y = 0}\\{z = 0}\end{array} \Rightarrow H(2;0;0)} \right.} \right.} \right.\)
Khi đó \(d(\Delta ,d) \le AH = \sqrt 3 \).
Dấu bằng xảy ra \( \Leftrightarrow \Delta \bot AH\).
Ta có \(\left\{ {\begin{array}{*{20}{l}}{\Delta \bot AH}\\{\Delta \subset (P)}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{\overrightarrow {{u_\Delta }} \bot \overrightarrow {AH} }\\{\overrightarrow {{u_\Delta }} \bot \overrightarrow {{n_P}} }\end{array} \Rightarrow } \right.} \right.\) VTCP của \(\Delta \) là \(\overrightarrow {{u_\Delta }} = \left[ {\overrightarrow {AH} ,\overrightarrow {{n_P}} } \right] = (0; - 2;2)\).
Suy ra phương trình của \(\Delta :\left\{ {\begin{array}{*{20}{l}}{x = 1}\\{y = 1 - 2t}\\{z = 1 + 2t}\end{array},(t \in \mathbb{R})} \right.\).
Ta thấy \(\Delta \) đi qua điểm \(N(1; - 1;3)\).
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án đúng là D
Phương pháp giải
Áp suất phân tử chất khí: \(p = \frac{1}{3}\rho \overline {{v^2}} \)
Lời giải
Áp suất mà khí đó tác dụng lên thành bình là:
\(p = \frac{1}{3}.\frac{m}{V}\overline {{v^2}} = \frac{1}{3}\rho \overline {{v^2}} \)
\[ \to p = \frac{1}{3}{.6.10^{ - 2}}{.500^2} = {5.10^3}\,(Pa)\]
Câu 2
Lời giải
Đáp án đúng là D
Phương pháp giải
Sử dụng công thức tính nhiệt lượng: Q = mcΔt
Phương trình cân bằng nhiệt: Qtỏa = Qthu
Lời giải
Diện tích tiếp xúc của từng cặp chất lỏng trong bài toàn là như nhau
Vậy nhiệt lượng truyền qua giữa chúng tỉ lệ với hiệu nhiệt độ với cùng một hệ số tỉ lệ là k
Ngăn 1 tỏa nhiệt sang ngăn 2 là Q12 = k(t1− t2)
Ngăn 1 tỏa nhiệt sang ngăn 3 là Q13 = k(t1 −t3)
Ngăn 2 tỏa nhiệt sang ngăn 3 là Q23 = k(t2 − t3)
Phương trình cân bằng nhiệt:
Ngăn 1 có \({Q_{12}} + {Q_{13}} = 2mc\Delta {t_1} \Rightarrow k\left( {2{t_2} - {t_2} - {t_3}} \right) = 2mc\Delta {t_1}\)
Ngăn 2 có \({Q_{12}} - {Q_{13}} = mc\Delta {t_2} \Rightarrow k\left( {{t_1} - 2{t_2} + {t_3}} \right) = mc\Delta {t_2}\)
Ngăn 3 có \({Q_{13}} + {Q_{23}} = mc\Delta {t_3} \Rightarrow k\left( {{t_1} + {t_2} - 2{t_3}} \right) = mc\Delta {t_3}\)
\( \Rightarrow \frac{{2{t_1} - {t_2} - {t_3}}}{{2\Delta {t_1}}} = \frac{{{t_1} - 2{t_2} + {t_3}}}{{\Delta {t_2}}} = \frac{{{t_1} + {t_2} - 2{t_3}}}{{\Delta {t_3}}}\)
\( \Rightarrow \frac{{2.65 - 35 - 20}}{{2.1}} = \frac{{65 - 2.35 + 20}}{{\Delta {t_2}}} = \frac{{65 + 35 - 2.20}}{{\Delta {t_3}}}\)
\[ \Rightarrow \Delta {t_2} = 0,{4^0}C\] và \[\Delta {t_3} = 1,{6^0}C\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập