Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\left[ { - 2;3} \right]\) và \(f'\left( x \right)\) có đồ thị như hình vẽ sau:
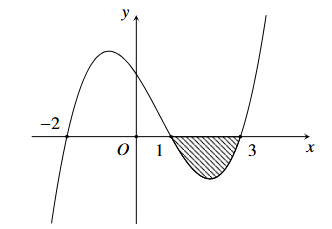
Biết \(\int\limits_{ - 2}^1 {f'\left( x \right)dx} = 3\) và diện tích phần gạch sọc trong hình vẽ \(S = \frac{5}{3}\). Giá trị \(f\left( 3 \right) - f\left( { - 2} \right)\) bằng bao nhiêu? (kết quả làm tròn đến hàng phần mười).
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\left[ { - 2;3} \right]\) và \(f'\left( x \right)\) có đồ thị như hình vẽ sau:
Biết \(\int\limits_{ - 2}^1 {f'\left( x \right)dx} = 3\) và diện tích phần gạch sọc trong hình vẽ \(S = \frac{5}{3}\). Giá trị \(f\left( 3 \right) - f\left( { - 2} \right)\) bằng bao nhiêu? (kết quả làm tròn đến hàng phần mười).
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 2 Toán 12 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án:
1,3
Trả lời: 1,3
Ta có \(\int\limits_{ - 2}^3 {f'\left( x \right)dx} = \int\limits_{ - 2}^1 {f'\left( x \right)dx} + \int\limits_1^3 {f'\left( x \right)dx} = 3 - \int\limits_1^3 {\left| {f'\left( x \right)} \right|dx} \)\( = 3 - \frac{5}{3} = \frac{4}{3}\).
Mà \(\int\limits_{ - 2}^3 {f'\left( x \right)dx} = \left. {f\left( x \right)} \right|_{ - 2}^3 = f\left( 3 \right) - f\left( { - 2} \right)\).
Do đó \(f\left( 3 \right) - f\left( { - 2} \right) \approx 1,3\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(\frac{{{\pi ^2}}}{4}\).
B. \(\frac{{{\pi ^2}}}{2}\).
C. \(\frac{\pi }{2}\).
D. \(\frac{\pi }{4}\).
Lời giải
Đáp án đúng là: B
Ta có \(V = \pi \int\limits_0^\pi {{{\sin }^2}xdx} = \left. {\pi \left( {\frac{x}{2} - \frac{{\sin 2x}}{4}} \right)} \right|_0^\pi = \pi .\frac{\pi }{2} = \frac{{{\pi ^2}}}{2}\).
Lời giải
Trả lời: 4
Ta có \(F\left( x \right) = \int {\left( {3{x^2} + \frac{1}{{2x + 1}}} \right)} dx = {x^3} + \frac{1}{2}\ln \left| {2x + 1} \right| + C\).
Vì \(F\left( 0 \right) = 0\) nên \(C = 0\).
Do đó \(F\left( x \right) = {x^3} + \frac{1}{2}\ln \left| {2x + 1} \right|\). Suy ra \(F\left( 1 \right) = {1^3} + \frac{1}{2}\ln \left| {2.1 + 1} \right| = 1 + \frac{1}{2}\ln 3\).
Do đó \(a + b + c = 1 + 1 + 2 = 4\).
Câu 3
a) Một vectơ chỉ phương của \(\Delta \) là \(\overrightarrow u = \left( {2;0; - 3} \right)\).
Đúng
Sai
b) Góc giữa \(\Delta \) và \(\left( P \right)\) là \(150^\circ \).
Đúng
Sai
c) Không có điểm chung nào giữa \(\Delta \) và \(\left( P \right)\).
Đúng
Sai
d) Hình chiếu của \(M\left( {1;2; - 1} \right)\) lên \(\left( P \right)\) là \(N\left( {1;2;1} \right)\).
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(5\).
B. \(9\).
C. \(6\).
D. \(\frac{3}{2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(\frac{1}{4}\).
B. \(\frac{{17}}{4}\).
C. \(\frac{{15}}{4}\).
D. \(\frac{{19}}{4}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập