Có bao nhiêu số nguyên dương \(y\) sao cho ứng với mỗi số \(y\) có không quá 5 số nguyên \(x\) thỏa mãn \(\left( {{3^{2x + 1}} + {{2.3}^x} - 1} \right)\left( {{3^x} - y} \right) \le 0\)
Có bao nhiêu số nguyên dương \(y\) sao cho ứng với mỗi số \(y\) có không quá 5 số nguyên \(x\) thỏa mãn \(\left( {{3^{2x + 1}} + {{2.3}^x} - 1} \right)\left( {{3^x} - y} \right) \le 0\)
Quảng cáo
Trả lời:
Đáp án
80.
Giải thích
Ta có: \(\left( {{3^{2x + 1}} + {{2.3}^x} - 1} \right)\left( {{3^x} - y} \right) \le 0 \Leftrightarrow \left[ {3.{{\left( {{3^x}} \right)}^2} + {{2.3}^x} - 1} \right]\left( {{3^x} - y} \right) \le 0\)
\( \Leftrightarrow \left( {{3^x} + 1} \right)\left( {{{3.3}^x} - 1} \right)\left( {{3^x} - y} \right) \le 0 \Leftrightarrow \left( {{3^{x + 1}} - 1} \right)\left( {{3^x} - y} \right) \le 0\) (do \({3^x} + 1 > 0,\forall x\)).
TH1. \({3^{x + 1}} - 1 \le 0 \Rightarrow x + 1 \le 0 \Leftrightarrow x \le - 1\) ta có \({3^x} - y \ge 0 \Rightarrow y \le {3^x} \le {3^{ - 1}} = \frac{1}{3}\) (vô lý vì \(y\) là số nguyên dương).
TH2. \({3^{x + 1}} - 1 \ge 0 \Rightarrow x + 1 \ge 0 \Leftrightarrow x \ge - 1\) ta có \({3^x} - y \le 0 \Rightarrow y \ge {3^x} \ge {3^{ - 1}} = \frac{1}{3}\) (luôn đúng vì \(y\) là số nguyên dương).
Để ứng với mỗi số \(y\) có không quá 5 số nguyên \(x\) thỏa mãn bất phương trình nên nghiệm \(x\) chỉ nằm trong khoảng \(\left\{ { - 1;0;1;2;3} \right\} \Rightarrow y < {3^4} = 81\).
Vậy có 80 số nguyên dương \(y\) thỏa mãn yêu cầu đề bài.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
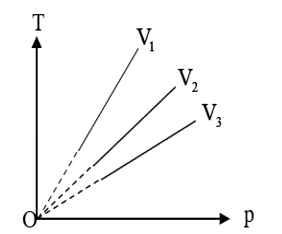
C. V3 < V2 < V1.
Lời giải
Đáp án
V3 < V2 < V1.
Giải thích
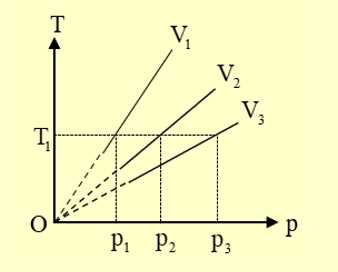
Ứng với nhiệt độ T1 ta có: p1 < p2 < p3
Do nhiệt độ không đổi, áp dụng định luật Boyle, ta có:
\({p_1}{V_1} = {p_2}{V_2} = {p_3}{V_3} \to {V_1} > {V_2} > {V_3}\).
Câu 2
Lời giải
Đáp án
\(\frac{{{a^3}\sqrt 3 }}{{96}}\).
Giải thích
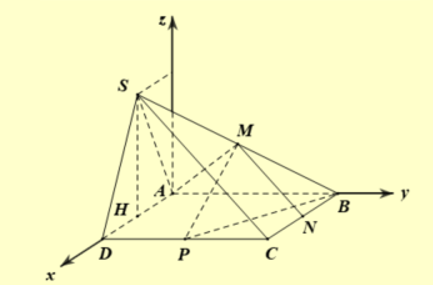
Gọi \(H\) là trung điểm của \(AD\). Do \(\Delta SAD\) đều nên \(SH \bot AD\).
Do \(\left( {SAD} \right) \bot \left( {ABCD} \right)\) nên \(SH \bot \left( {ABCD} \right)\)
Dựng đường thẳng Az vuông góc với \(\left( {ABCD} \right)\), ta có \(AD,AB,Az\) là ba tia đôi một vuông góc nhau. Chọn hệ trục \(Oxyz\) như hình vẽ (\(O \equiv A\)).
Không mất tính tổng quát, chọn \(a = 1\). Ta có:
\(A\left( {0;0;0} \right),S\left( {\frac{1}{2};0;\frac{{\sqrt 3 }}{2}} \right),M\left( {\frac{1}{4};\frac{1}{2};\frac{{\sqrt 3 }}{4}} \right),B\left( {0;1;0} \right),P\left( {1;\frac{1}{2};0} \right),C\left( {1;1;0} \right),N\left( {\frac{1}{2};1;0} \right)\)
\( \Rightarrow \overrightarrow {CP} = \left( {0; - \frac{1}{2};0} \right),\overrightarrow {CN} = \left( { - \frac{1}{2};0;0} \right) \Rightarrow \left[ {\overrightarrow {CP} ,\overrightarrow {CN} } \right] = \left( {0;0; - \frac{1}{4}} \right)\) và \(\overrightarrow {CM} = \left( { - \frac{3}{4}; - \frac{1}{2};\frac{{\sqrt 3 }}{4}} \right)\)
Nên \({V_{CMNP}} = \frac{1}{6}\left| {\left[ {\overrightarrow {CP} ,\overrightarrow {CN} } \right].\overrightarrow {CM} } \right| = \frac{{\sqrt 3 }}{{96}}\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.