Cho đường tròn (O:R) và dây cung BC cố định của đường tròn thỏa mãn BC\( < 2{\rm{R}}.{\rm{\;}}\)Một điểm A di chuyển trên (O:R) sao cho tam giác ABC có ba góc nhọn. Các đường cao AD, BE, CF của tam giác ABC cắt nhau tại H. Đường phân giác của \(\widehat {{\rm{CHE}}}{\rm{\;k\'e o\;d\`a i\;}}\)về hai phía cắt AB và AC lần lượt tại M,N.
1. Chứng minh tam giác AMN cân tại A.
2. Gọi I , P, Q, J lần lượt là hình chiếu của D trên cạnh AB, BE, CF, AC. Chứng minh rằng bốn điểm I, P, Q, J cùng nằm trên một đường thẳng vuông góc với AO.
3. Đường tròn ngoại tiếp tam giác AMN cắt đường phân giác trong của \(\widehat {{\rm{BAC}}}\) tại điểm thứ hai K. chứng minh rằng HK luôn đi qua một điểm cố định.
Cho đường tròn (O:R) và dây cung BC cố định của đường tròn thỏa mãn BC\( < 2{\rm{R}}.{\rm{\;}}\)Một điểm A di chuyển trên (O:R) sao cho tam giác ABC có ba góc nhọn. Các đường cao AD, BE, CF của tam giác ABC cắt nhau tại H. Đường phân giác của \(\widehat {{\rm{CHE}}}{\rm{\;k\'e o\;d\`a i\;}}\)về hai phía cắt AB và AC lần lượt tại M,N.
1. Chứng minh tam giác AMN cân tại A.
2. Gọi I , P, Q, J lần lượt là hình chiếu của D trên cạnh AB, BE, CF, AC. Chứng minh rằng bốn điểm I, P, Q, J cùng nằm trên một đường thẳng vuông góc với AO.
3. Đường tròn ngoại tiếp tam giác AMN cắt đường phân giác trong của \(\widehat {{\rm{BAC}}}\) tại điểm thứ hai K. chứng minh rằng HK luôn đi qua một điểm cố định.
Quảng cáo
Trả lời:
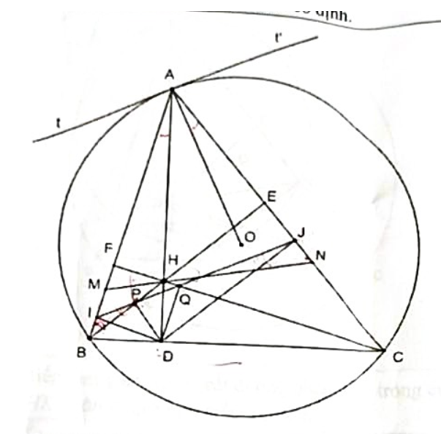
4.1. chứng minh tam giác AMN cân tại A.
Vì BE\({\rm{\;}} \bot {\rm{AC}} = {\rm{E\;n\^e n\;HEC}} = 90^\circ \)
Vì CF \( \bot {\rm{AB}} = {\rm{F\;n\^e n\;HFB}} = 90^\circ \)
\( \Rightarrow {\rm{FMH}} + {\rm{MHF}} = 90^\circ ;{\rm{ENH}} + {\rm{NHE}} = 90^\circ {\rm{\;}}\left( 1 \right)\)
Vì HN là phân giác của góc CHE nên CHN = NHE
Lại có CHN=MHF ( đối đỉnh) nên NHE = MHF (2)
Từ (1) và (2) suy ra FMH = ENH hay AMN =ANM
Vậy \(\Delta {\rm{AMN\;c\^a n\;tai\;A}}.\)
2. Chỉ ra tứ giác BIPD nội tiếp nên IBD + IPD =180\(^\circ {\rm{\;}}\left( 3 \right)\)
Chỉ ra IBD = FHA ( cùng phụ với góc FAH);
Lại có FHA = QHD( đối đỉnh)\( \Rightarrow {\rm{IBD}} = {\rm{QHD}};\)
Chỉ ra tứ giác DPHQ nội tiếp nên QHD = QPD\( \Rightarrow {\rm{IBD}} = {\rm{QPD\;}}\left( 4 \right)\)
Từ (3) và (4) suy ra QPD + IPD =1800 nên ba điểm I, P, Q thẳng hàng
Chứng minh tương tự ta được P, Q, J thẳng hàng.
Vậy 4 điểm I, P, Q, J thẳng hàng.
Từ tứ giác BIPD nội tiếp chỉ ra MIP = PDB
Lại có PD//AC (cùng vuông góc với BE) nên PDB = ACB
Qua A kẻ tiếp tuyến tAt’ của (O)suy ra AO
Suy ra tAI = AIP
Mà hai góc này ở vị trí so le trong nên IP//At
3.
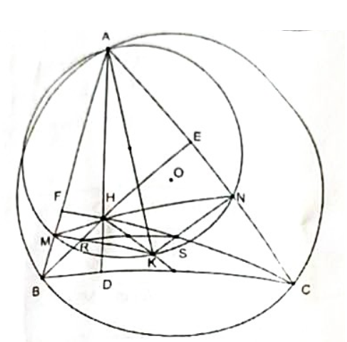
Vì tam giác AMN cân tại A và AK là phân giác góc MAN nên AK là trung trực của MN suy ra AK là đường kính của đường tròn ngoại tiếp AMN
AKM = ANK = 90\(^\circ \Rightarrow {\rm{KM}}\)//CF ; KN //BE
Gọi R = KM\( \cap {\rm{BH}};{\rm{s}} = {\rm{KN}} \cap {\rm{HC\;}} \Rightarrow {\rm{HRKS\;\;l\`a \;h\`i nh\;b\`i nh\;h\`a nh}}\)suy ra HK đi quả trung điểm của RS (5)
Từ MR//FH\( \Rightarrow \frac{{{\rm{HR}}}}{{{\rm{RB}}}} = \frac{{{\rm{FM}}}}{{{\rm{MB}}}};\)
Vì HN là phân giác của góc CHE nên HM là phân giác của góc BHF \( \Rightarrow \frac{{{\rm{FM}}}}{{{\rm{MB}}}} = \frac{{{\rm{FH}}}}{{{\rm{HB}}}}\)
Từ SN//HE \( \Rightarrow \frac{{{\rm{HS}}}}{{{\rm{SC}}}} = \frac{{{\rm{EN}}}}{{{\rm{NC}}}};\)
Vì HN là phân giác của góc CHE nên \(\frac{{{\rm{EN}}}}{{{\rm{NC}}}} = \frac{{{\rm{HE}}}}{{{\rm{HC}}}}\)
Chỉ ra \(\Delta {\rm{FHB}}\~\Delta {\rm{EHC}}\left( {{\rm{\;\;g\'o c}} - {\rm{g\'o c}}} \right) \Rightarrow \frac{{{\rm{FH}}}}{{{\rm{NC}}}} = \frac{{{\rm{HE}}}}{{{\rm{HC}}}}\)
\( \Rightarrow \frac{{{\rm{HR}}}}{{{\rm{RB}}}} = \frac{{{\rm{HS}}}}{{{\rm{SC}}}} \Rightarrow {\rm{RS}}\)//BC (6)
Từ
(5) và (6) suy ra HK luôn đi qua trung điểm của BC ( cố định).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
1. \({{\rm{x}}^3} + {{\rm{y}}^3} + {{\rm{x}}^2}\left( {3{\rm{y}} + 2{\rm{z}}} \right) + {{\rm{y}}^2}\left( {3{\rm{x}} + 2{\rm{z}}} \right) + {{\rm{z}}^2}\left( {{\rm{x}} + {\rm{y}}} \right) + 4{\rm{xyz}} = 2023.\)
\( \Leftrightarrow {{\rm{x}}^3} + {{\rm{y}}^3} + 3{{\rm{x}}^2}{\rm{y}} + 2{{\rm{x}}^2}{\rm{z}} + 3{\rm{x}}{{\rm{y}}^2} + 2{{\rm{y}}^2}{\rm{z}} + {{\rm{z}}^2}{\rm{x}} + {{\rm{z}}^2}{\rm{y}} + 4{\rm{xyz}} = 2023\)
\( \Leftrightarrow \left( {{{\rm{x}}^3} + 3{{\rm{x}}^2}{\rm{y}} + 3{\rm{x}}{{\rm{y}}^2} + {{\rm{y}}^3}} \right) + \left( {2{{\rm{x}}^2}{\rm{z}} + 2{{\rm{y}}^2}{\rm{z}} + 4{\rm{xyz}}} \right) + \left( {{{\rm{z}}^2}{\rm{x}} + {{\rm{z}}^2}{\rm{y}}} \right) = 2023\)
\( \Leftrightarrow {\left( {{\rm{x}} + {\rm{y}}} \right)^3} + 2{\rm{z}}{\left( {{\rm{x}} + {\rm{y}}} \right)^2} + {{\rm{z}}^2}\left( {{\rm{x}} + {\rm{y}}} \right) = 2023\)
\( \Leftrightarrow \left( {{\rm{x}} + {\rm{y}}} \right)\left[ {{{\left( {{\rm{x}} + {\rm{y}}} \right)}^2} + 2{\rm{z}}\left( {{\rm{x}} + {\rm{y}}} \right) + {{\rm{z}}^2}} \right] = 2023\)
\( \Leftrightarrow \left( {{\rm{x}} + {\rm{y}}} \right){\left( {{\rm{x}} + {\rm{y}} + {\rm{z}}} \right)^2} = {7.17^2}\)
Vì x,y,z nguyên dương nếu ta có x + y + z\(\left\{ {\begin{array}{*{20}{c}}{x + y = 7}\\{x + y + z = 17}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{c}}{x + y = 7}\\{z = 10}\end{array}} \right.} \right.\)
Có x + y = 7 mà x, y nguyên dương nên ta có
|
x |
1 |
2 |
3 |
4 |
5 |
6 |
|
y |
6 |
5 |
4 |
3 |
2 |
1 |
KL: các bộ số cần tìm là (1;6;10);(3;4;10);(94;3;10);(5;2;10);(6;1;10)
2. Xét tất cả các cách nối 2024 cặp điểm (đỏ với xanh) bằng 2024 đoạn thẳng. các cách nối như vậy luôn luôn tồn tại do chỉ có 2024 cặp điểm nên số tất cả các cách nối như vậy là hữu hạn.
Do đó, tìm được một cách nối có tổng độ dài bằng các đoạn thẳng là ngắn nhất.
Ta chứng minh rằng đây là một cách nối phải tìm
Thật vậy , giả sữ ngược lại ta có hai đoạn thẳng AX và BY mà cắt nhau tại điểm O (giả sử A và B tô màu đỏ, còn X và Y tô màu xanh).khi đó nếu ta thay đoạn thẳng AX và BY bằng hai đoạn thẳng AY và BX, các đoạn thẳng khác giữ nguyên thì ta có cách nối này có tính chất:
AY+BX \( < \left( {{\rm{AO}} + {\rm{OY}}} \right) = \left( {{\rm{AO}} + {\rm{OX}}} \right) + \left( {{\rm{BO}} + {\rm{OY}}} \right) \Rightarrow {\rm{AY}} + {\rm{BX}} < {\rm{AX}} + {\rm{BY}}\)
Như vậy , việc thay hai đoạn thẳng AX và BY bằng hai đoạn thẳng AY và BX , ta nhận được một cách nối mới có tổng độ dài các đoạn thẳng là nhỏ hơn. Vô lý, vì trái với giả thiết là đã chọn một cách nối có tổng các độ dài là bé nhất.
Điều vô lý chứng tỏ: cách nối có tổng độ dài các đoạn thẳng là ngắn nhất là không có điểm chung.
Lời giải
Từ giả thiết x + y + z = xyz, ta có \(\frac{1}{{{\rm{xy}}}} = \frac{1}{{{\rm{yz}}}} = \frac{1}{{{\rm{xz}}}} = 1.\)
Dặt a=\(\frac{1}{{\rm{x}}};{\rm{b}} = \frac{1}{{\rm{y}}};{\rm{c}} = \frac{1}{{\rm{z}}} \Rightarrow {\rm{a}},{\rm{b}},{\rm{c}} > 0;\)
Giả thiết trở thành ab + bc + ca = 1; P =\(\frac{{\rm{a}}}{{\sqrt {1 + {{\rm{a}}^2}} }} + \frac{{\rm{b}}}{{\sqrt {1 + {{\rm{b}}^2}} }} + \frac{{\rm{c}}}{{\sqrt {1 + {{\rm{c}}^2}} }}\)
Đẻ ý rằng:
\({{\rm{a}}^2} + 1 = {{\rm{a}}^2} + {\rm{ab}} + {\rm{bc}} + {\rm{ca}} = \left( {{\rm{a}} + {\rm{b}}} \right)\left( {{\rm{a}} + {\rm{c}}} \right)\)
\({{\rm{b}}^2} + 1 = {{\rm{b}}^2} + {\rm{ab}} + {\rm{bc}} + {\rm{ca}} = \left( {{\rm{b}} + {\rm{a}}} \right)\left( {{\rm{b}} + {\rm{c}}} \right)\)
\({{\rm{c}}^2} + 1 = {{\rm{c}}^2} + {\rm{ab}} + {\rm{bc}} + {\rm{ca}} = \left( {{\rm{c}} + {\rm{a}}} \right)\left( {{\rm{c}} + {\rm{b}}} \right)\)
Lúc này ta có:
P=\(\frac{{\rm{a}}}{{\sqrt {\left( {{\rm{a}} + {\rm{b}}} \right)\left( {{\rm{a}} + c} \right)} }} + \frac{{\rm{b}}}{{\sqrt {\left( {{\rm{b}} + {\rm{a}}} \right)\left( {{\rm{b}} + c} \right)} }} + \frac{{\rm{c}}}{{\sqrt {\left( {{\rm{c}} + {\rm{a}}} \right)\left( {{\rm{c}} + {\rm{b}}} \right)} }}\)
=\(\sqrt {\frac{{\rm{a}}}{{{\rm{a}} + {\rm{b}}}}.} \sqrt {\frac{{\rm{a}}}{{{\rm{a}} + {\rm{c}}}}} + \sqrt {\frac{{\rm{b}}}{{{\rm{b}} + {\rm{a}}}}.} \sqrt {\frac{{\rm{b}}}{{{\rm{b}} + {\rm{c}}}}} + \sqrt {\frac{{\rm{c}}}{{{\rm{c}} + {\rm{a}}}}.} \sqrt {\frac{{\rm{c}}}{{{\rm{c}} + {\rm{b}}}}} {\rm{\;}}\)
Theo bất đẳng thức Cô-si (AM-GM), ta có:
P\( \le \frac{1}{2}\left( {\frac{{\rm{a}}}{{{\rm{a}} + {\rm{b}}}} + \frac{{\rm{a}}}{{{\rm{a}} + {\rm{c}}}} + \frac{{\rm{b}}}{{{\rm{b}} + {\rm{a}}}} + \frac{{\rm{b}}}{{{\rm{b}} + {\rm{c}}}} + \frac{{\rm{c}}}{{{\rm{c}} + {\rm{a}}}} + \frac{{\rm{c}}}{{{\rm{c}} + {\rm{b}}}}} \right)\) hay P\( \le \frac{3}{2}\).
Dấu = xảy ra khi và chỉ khi a = b = c =\(\frac{1}{{\sqrt 3 }}{\rm{\;hay\;x}} = {\rm{y}} = {\rm{z}} = \sqrt 3 \)
Vậy giá trị lớn nhất của P =\(\frac{3}{2}{\rm{\;}} \Leftrightarrow {\rm{x}} = {\rm{y}} = {\rm{z}} = \sqrt 3 .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.