1. Cho tam giác \(ABC\) nhọn nội tiếp đường tròn \(\left( O \right)\), \(AB < AC\), có các đường cao \(BE\) và \(CF\).
Các tiếp tuyến của đường tròn (O) tại B và C cắt nhau tại S. Gọi M là giao điểm của BC và SO.
a. Chứng minh rằng tam giác EAB đồng dạng với tam giác MBS, từ đó suy ra tam giác
AEM đồng dạng với tam giác ABS.
b. Gọi N là giao điểm của AM và EF, P là giao điểm của SA và BC. Chứng minh rằng NP
vuông góc với BC.
2. Cho hình chữ nhật ABCD. Lấy các điểm E, F thuộc cạnh AB (E nằm giữa A, F); G, H
thuộc cạnh BC (C nằm giữa B, H); I, J thuộc cạnh CD (I nằm giữa C, J); K, M thuộc cạnh DA (K nằm giữa D, M) sao cho E, F, G, H, I, J, K, M đôi một phân biệt và khác các đỉnh của hình chữ nhật ABCD, đồng thời hình đa giác EFGHIJKM có các góc bằng nhau. Chứng minh rằng nếu độ dài các cạnh của hình đa giác EFGHIJKM là các số hữu tỉ (theo đơn vị cm) thì EF = IJ.
1. Cho tam giác \(ABC\) nhọn nội tiếp đường tròn \(\left( O \right)\), \(AB < AC\), có các đường cao \(BE\) và \(CF\).
Các tiếp tuyến của đường tròn (O) tại B và C cắt nhau tại S. Gọi M là giao điểm của BC và SO.
a. Chứng minh rằng tam giác EAB đồng dạng với tam giác MBS, từ đó suy ra tam giác
AEM đồng dạng với tam giác ABS.
b. Gọi N là giao điểm của AM và EF, P là giao điểm của SA và BC. Chứng minh rằng NP
vuông góc với BC.
2. Cho hình chữ nhật ABCD. Lấy các điểm E, F thuộc cạnh AB (E nằm giữa A, F); G, H
thuộc cạnh BC (C nằm giữa B, H); I, J thuộc cạnh CD (I nằm giữa C, J); K, M thuộc cạnh DA (K nằm giữa D, M) sao cho E, F, G, H, I, J, K, M đôi một phân biệt và khác các đỉnh của hình chữ nhật ABCD, đồng thời hình đa giác EFGHIJKM có các góc bằng nhau. Chứng minh rằng nếu độ dài các cạnh của hình đa giác EFGHIJKM là các số hữu tỉ (theo đơn vị cm) thì EF = IJ.
Quảng cáo
Trả lời:
|
1. Học sinh vẽ đúng hình để làm được ý a |
|
|
a. Ta có \(OS \bot BC\)tại trung điểm M của BC. Nên \(\widehat {BEA} = \widehat {SMB} = {90^0}\). Mà . Suy ra \(\Delta EAB\) đồng dạng \(\Delta MBS\). |
|
|
Hai tam giác EAB, MBS đồng dạng nên \(\frac{{AB}}{{AE}} = \frac{{BS}}{{BM}}\). Tam giác BEC vuông tại E, EM là trung tuyến nên BM = ME. Suy ra \(\frac{{AB}}{{AE}} = \frac{{BS}}{{ME}}\,\,\,\left( 1 \right)\)
|
|
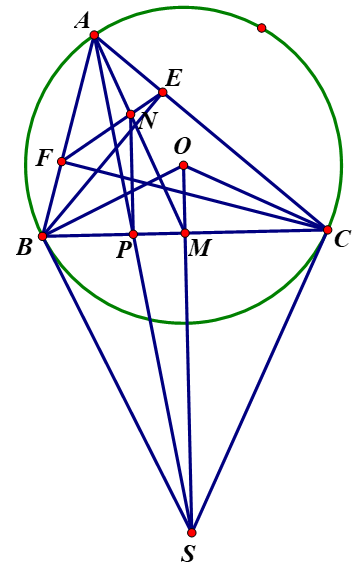 |
Tam giác MEC cân tại M, nên \(\widehat {MEC} = \widehat {MCE}\). Mặt khác \(\begin{array}{l}\widehat {ABS} + \widehat {ACB} = {180^0} = \widehat {AEM} + \widehat {MEC}\\ = \widehat {AEM} + \widehat {ACB}\\ \Rightarrow \widehat {ABS} = \widehat {AEM}\,\,(2).\end{array}\) Từ (1), (2) suy ra hai tam giác AEM, ABS đồng dạng. |
|
b. Hai tam giác AEM, ABS đồng dạng nên \(\widehat {BAP} = \widehat {EAN}\); \(\widehat {AME} = \widehat {ASB}\,\,\,(3)\). Mà tứ giác BCEF nội tiếp đường tròn đường kính BC nên \(\widehat {ABP} = \widehat {AEN}\). Suy ra hai tam giác AEN, ABP đồng dạng, dẫn tới \(\frac{{AN}}{{AP}} = \frac{{NE}}{{BP}}\,\,(4)\) |
|
|
Ta có: \(\widehat {NEM} + \widehat {ABC} + \widehat {ACB} = \widehat {NEM} + \widehat {AEN} + \widehat {MEC} = {180^0}.\) Suy ra: \(\widehat {NEM} = \widehat {BAC} = \widehat {SBP}\,\,\,(5)\) Từ (3) và (5) suy ra hai tam giác EMN, BSP đồng dạng. Do đó \(\frac{{NE}}{{BP}} = \frac{{MN}}{{PS}}\,\,\,\,(6)\) |
|
|
Từ (4) và (6) suy ra \(\frac{{AN}}{{AP}} = \frac{{NM}}{{PS}} \Rightarrow \frac{{AN}}{{MN}} = \frac{{AP}}{{PS}} \Rightarrow NP//MS\). Mà \(SM \bot BC \Rightarrow NP \bot BC\). |
|
|
2. Gọi \(EF = a;\,\,FG = b;\,\,GH = c;\,\,HI = d;\,\,IJ = e;\,\,JK = f;\,\,KM = g;\,\,ME = h\)(theo đơn vị cm, với \(a,b,c,d,e,f,g,,h\)là các số hữu tỉ dương). Do các góc của hình bát giác EFGHIJKM bằng nhau nên mỗi góc trong của hình bát giác đó có số đo là \(\frac{{(8 - 2){{.180}^0}}}{8} = {135^0}\). |
|
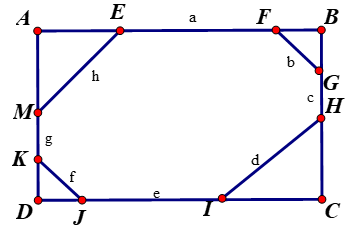 |
Suy ra mỗi góc ngoài của hình bát giác này là \({180^0} - {135^0} = {45^0}.\) Do đó các tam giác MAE; FBG; CIH; DKJ là các tam giác vuông cân.
|
|
Ta có: \(MA = ME = \frac{h}{{\sqrt 2 }};\,\,BF = BG = \frac{b}{{\sqrt 2 }};\,\,CH = CI = \frac{d}{{\sqrt 2 }};\,\,DK = DJ = \frac{f}{{\sqrt 2 }}.\) Vì AB = CD nên \(\frac{h}{{\sqrt 2 }} + a + \frac{b}{{\sqrt 2 }} = \frac{f}{{\sqrt 2 }} + e + \frac{d}{{\sqrt 2 }} \Leftrightarrow (e - a)\sqrt 2 = h + b - f - d.\) |
|
|
Nếu \(e - a \ne 0\)thì \(\sqrt 2 = \frac{{h + b - f - d}}{{e - a}},\) điều này vô lí, do \(\sqrt 2 \) là số vô tỉ, còn \(\frac{{h + b - f - d}}{{e - a}},\) là số hữu tỉ. Vậy \(e - a = 0 \Leftrightarrow e = a\) hay EF = IJ (đpcm) |
|
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
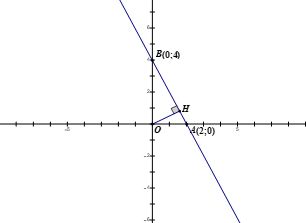
2. Vẽ đường thẳng d là đồ thị của hàm số y = 2x – 4
Đường thẳng d cắt trục Ox tại A(2; 0), cắt trục Oy tại B(0; 4)Tính được OA = 2; OB = 4. Gọi H là hình chiếu của O trên AB. Ta có
\(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} = \frac{1}{4} + \frac{1}{{16}} = \frac{5}{{16}} \Rightarrow OH = \frac{{4\sqrt 5 }}{5}\)
Vậy khoảng cách từ gốc tọa độ O đến đường thẳng d là \(OH = \frac{{4\sqrt 5 }}{5}\).Lời giải
1. Ta sẽ chứng minh \(\left( {3 - 2a} \right)\left( {3 - 2b} \right)\left( {3 - 2c} \right) \le abc\,\,(1).\)
Nếu \(\left( {3 - 2a} \right)\left( {3 - 2b} \right)\left( {3 - 2c} \right) \le 0\) thì (1) đúng
...........................................................
Ta có
\(\left. \begin{array}{l}\left( {3 - 2a} \right)\left( {3 - 2b} \right) \le {\left( {\frac{{3 - 2a + 3 - 2b}}{2}} \right)^2} = {c^2}\\\left( {3 - 2a} \right)\left( {3 - 2c} \right) \le {\left( {\frac{{3 - 2a + 3 - 2c}}{2}} \right)^2} = {b^2}\\\left( {3 - 2c} \right)\left( {3 - 2b} \right) \le {\left( {\frac{{3 - 2c + 3 - 2b}}{2}} \right)^2} = {a^2}\end{array} \right\} \Rightarrow \left( {3 - 2a} \right)\left( {3 - 2b} \right)\left( {3 - 2c} \right) \le abc\,\,.\)
Dấu “=” ở (1) xảy ra khi a = b = c = 1.
Từ (1) ta có \(27 - 9\left( {2a + 2b + 2c} \right) + 3\left( {4ab + 4bc + 4ca} \right) - 8abc \le abc\)
\(\begin{array}{l} \Leftrightarrow 27 - 9.6 + 12\left( {ab + bc + ac} \right) - 8abc \le abc\,\,(do\,\,a + b + c = 3)\\ \Leftrightarrow abc \ge \frac{4}{3}\left( {ab + bc + ca} \right) - 3\end{array}\)
Lúc này
Dấu “=” xảy ra khi a = b = c = 1.
2. Ta chứng minh bài toán bằng phương pháp phản chứng.
Giả sử tồn tại đường tròn tâm O bán kính bằng 1 có thể chứa được n điểm trong 2008 điểm đã cho, \(n \in N,\,\,n \ge 6\). Gọi 6 điểm trong số n điểm đó là A, B, M, N, E, F.
TH1: Một điểm trong các điểm A, B, M, N, E, F trùng với O. Khi đó 5 điểm còn lại sẽ cách tâm O một khoảng bé hơn hoặc bằng 1, mâu thuẫn với giả thiết.
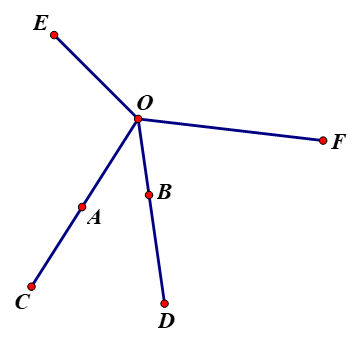
TH2: Các điểm A, B, M, N, E, F không trùng tâm O. Khi đó vẽ các bán kính đi qua 6 điểm trên.
Vì có 6 bán kính nên tồn tại 2 bán kính tạo thành một góc bé hơn hoặc bằng 600. Giả sử 2 bán kính OC và OD lần lượt đi qua A và B, \(\widehat {AOB} \le {60^0}\).
Ta có
\(\widehat {OBA} + \widehat {OAB} = {180^0} - \widehat {AOB} \ge {120^0}\).
Suy ra một trong hai góc \(\widehat {OBA},\,\widehat {OAB}\) phải lớn hơn hoặc bằng 600. Không mất tính tổng quát giả sử \(\widehat {OBA} \ge {60^0},\,\,suy\,ra\)
\(AB \le OA \le OC = 1\), mâu thuẫn với giải thiết. Từ hai trường hợp trên chứng tỏ không tồn tại hình tròn tâm O bán kính bằng 1 chứa được nhiều hơn 5 điểm trong số 2008 điểm đã cho. Vậy mỗi hình tròn có bán kính bằng 1 chỉ chứa không quá 5 điểm trong 2008 điểm đã cho.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.