1. Cho các số nguyên dương \(x,\,y,\,z\) thỏa mãn \({x^3} + {y^3} + {z^3} = 18(x + y + z)\).
2. Chứng minh rằng \(x + y + z\,\,\)chia hết cho 6.
Tìm giá trị lớn nhất của biểu thức F = xyz.
1. Cho các số nguyên dương \(x,\,y,\,z\) thỏa mãn \({x^3} + {y^3} + {z^3} = 18(x + y + z)\).
2. Chứng minh rằng \(x + y + z\,\,\)chia hết cho 6.
Tìm giá trị lớn nhất của biểu thức F = xyz.Quảng cáo
Trả lời:
1. Từ giả thiết ta có \(\left( {{x^3} - x} \right) + \left( {{y^3} - y} \right) + \left( {{z^3} - z} \right) = 17(x + y + z)\)
Tích của ba số nguyên liên tiếp luôn chia hết cho 6 nên \({x^3} - x = (x - 1)x(x + 1) \vdots 6\)
Tương tự \({y^3} - y \vdots 6,\,\,{z^3} - z \vdots 6 \Rightarrow \,\,\,17(x + y + z)\, \vdots 6\)
Mà 17 và 6 nguyên tố cùng nhau nên \(x + y + z\, \vdots 6\)
2. Ta có \(x + y + z\, = \,6m,\,\,\,{x^3} + {y^3} + {z^3} = 108m,\) với \(m \in {N^*}\).
Vì \(\frac{{{x^3} + {y^3} + {z^3}}}{3} \ge {\left( {\frac{{x + y + z}}{3}} \right)^3}\) nên \(\frac{{108m}}{3} \ge {\left( {\frac{{6m}}{3}} \right)^3} \Leftrightarrow {m^2} \le \frac{9}{2},\,\,suy\,\,ra\,m \le 2\)
Lúc này \(F = xyz \le {\left( {\frac{{x + y + z}}{3}} \right)^3} \le {\left( {\frac{{12}}{3}} \right)^3} = 64\,\,\,\,(1)\)
Từ \({x^3} + {y^3} + {z^3} - 3xyz = \left( {x + y + z} \right)\left( {{x^2} + {y^2} + {z^2} - xy - yz - zx} \right)\,\,\,suy\,\,ra\)
\(108m - 3F = 6m\left( {36{m^2} - 3\left( {xy + yz + zx} \right)} \right) \Leftrightarrow F = 36m - 6m\left( {12{m^2} - \left( {xy + yz + zx} \right)} \right).\)
Do đó \(F\, \vdots \,6\,\,\,\,(2)\). Từ (1) và (2) suy ra \(F \le 60\,\,(3)\).
Đẳng thức ở (3) xảy ra, chẳng hạn khi
\(\left\{ \begin{array}{l}x + y + z = 12\\60 = 72 - 12\left( {48 - \left( {xy + yz + zx} \right)} \right)\\xyz = 60\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x + y + z = 12\\xy + yz + zx = 47\\xyz = 60\end{array} \right. \Leftrightarrow \left( {x;y;z} \right)\) là hoán vị của \(\left( {3;4;5} \right)\)
Vậy giá trị lớn nhất của F là 60, đạt được chẳng hạn khi \(\left( {x;y;z} \right)\) là hoán vị của \(\left( {3;4;5} \right)\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
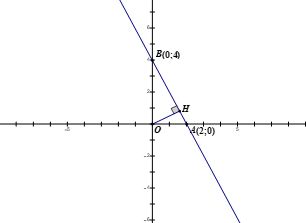
2. Vẽ đường thẳng d là đồ thị của hàm số y = 2x – 4
Đường thẳng d cắt trục Ox tại A(2; 0), cắt trục Oy tại B(0; 4)Tính được OA = 2; OB = 4. Gọi H là hình chiếu của O trên AB. Ta có
\(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} = \frac{1}{4} + \frac{1}{{16}} = \frac{5}{{16}} \Rightarrow OH = \frac{{4\sqrt 5 }}{5}\)
Vậy khoảng cách từ gốc tọa độ O đến đường thẳng d là \(OH = \frac{{4\sqrt 5 }}{5}\).Lời giải
1. Ta sẽ chứng minh \(\left( {3 - 2a} \right)\left( {3 - 2b} \right)\left( {3 - 2c} \right) \le abc\,\,(1).\)
Nếu \(\left( {3 - 2a} \right)\left( {3 - 2b} \right)\left( {3 - 2c} \right) \le 0\) thì (1) đúng
...........................................................
Ta có
\(\left. \begin{array}{l}\left( {3 - 2a} \right)\left( {3 - 2b} \right) \le {\left( {\frac{{3 - 2a + 3 - 2b}}{2}} \right)^2} = {c^2}\\\left( {3 - 2a} \right)\left( {3 - 2c} \right) \le {\left( {\frac{{3 - 2a + 3 - 2c}}{2}} \right)^2} = {b^2}\\\left( {3 - 2c} \right)\left( {3 - 2b} \right) \le {\left( {\frac{{3 - 2c + 3 - 2b}}{2}} \right)^2} = {a^2}\end{array} \right\} \Rightarrow \left( {3 - 2a} \right)\left( {3 - 2b} \right)\left( {3 - 2c} \right) \le abc\,\,.\)
Dấu “=” ở (1) xảy ra khi a = b = c = 1.
Từ (1) ta có \(27 - 9\left( {2a + 2b + 2c} \right) + 3\left( {4ab + 4bc + 4ca} \right) - 8abc \le abc\)
\(\begin{array}{l} \Leftrightarrow 27 - 9.6 + 12\left( {ab + bc + ac} \right) - 8abc \le abc\,\,(do\,\,a + b + c = 3)\\ \Leftrightarrow abc \ge \frac{4}{3}\left( {ab + bc + ca} \right) - 3\end{array}\)
Lúc này
Dấu “=” xảy ra khi a = b = c = 1.
2. Ta chứng minh bài toán bằng phương pháp phản chứng.
Giả sử tồn tại đường tròn tâm O bán kính bằng 1 có thể chứa được n điểm trong 2008 điểm đã cho, \(n \in N,\,\,n \ge 6\). Gọi 6 điểm trong số n điểm đó là A, B, M, N, E, F.
TH1: Một điểm trong các điểm A, B, M, N, E, F trùng với O. Khi đó 5 điểm còn lại sẽ cách tâm O một khoảng bé hơn hoặc bằng 1, mâu thuẫn với giả thiết.
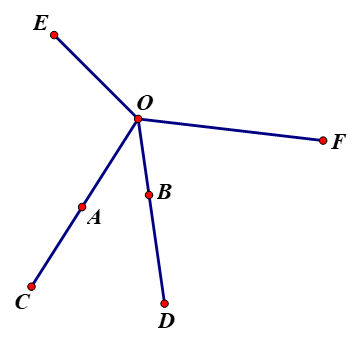
TH2: Các điểm A, B, M, N, E, F không trùng tâm O. Khi đó vẽ các bán kính đi qua 6 điểm trên.
Vì có 6 bán kính nên tồn tại 2 bán kính tạo thành một góc bé hơn hoặc bằng 600. Giả sử 2 bán kính OC và OD lần lượt đi qua A và B, \(\widehat {AOB} \le {60^0}\).
Ta có
\(\widehat {OBA} + \widehat {OAB} = {180^0} - \widehat {AOB} \ge {120^0}\).
Suy ra một trong hai góc \(\widehat {OBA},\,\widehat {OAB}\) phải lớn hơn hoặc bằng 600. Không mất tính tổng quát giả sử \(\widehat {OBA} \ge {60^0},\,\,suy\,ra\)
\(AB \le OA \le OC = 1\), mâu thuẫn với giải thiết. Từ hai trường hợp trên chứng tỏ không tồn tại hình tròn tâm O bán kính bằng 1 chứa được nhiều hơn 5 điểm trong số 2008 điểm đã cho. Vậy mỗi hình tròn có bán kính bằng 1 chỉ chứa không quá 5 điểm trong 2008 điểm đã cho.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.