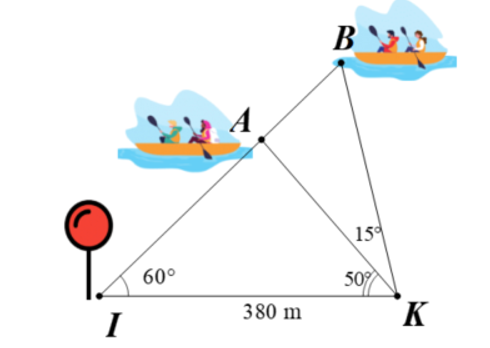
Hội đua ghe truyền thống tỉnh Thừa Thiên Huế là một ngày lễ hội mới được tổ chức sau ngày Giải phóng miền Nam 1975. Hội được tổ chức trong một ngày, địa điểm đua là bờ sông Hương trước trường Quốc Học. Trong cuộc đua ghe, ghe \(A\) và ghe \(B\) ở vị trí như hình vẽ. Điểm \(K\) là vị trí khán giả đứng xem và quan sát thấy ghe \(A\) và ghe \(B\) theo các góc tạo với bờ \(IK\) lần lượt là \({50^ \circ }\) và \({65^ \circ }\). Điểm \(I\) là đích đến của cuộc đua. Lúc ghe \(A\), ghe \(B\) và đích \(I\) thẳng hàng, từ điểm \(I\) quan sát thấy ghe \(A\) và ghe \(B\) tạo với bờ một góc bằng \({60^ \circ }\). Tính khoảng cách giữa hai ghe thuyền (đơn vị: mét, làm tròn đến chữ số thập phân thứ hai).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án
110, 65.
Giải thích
Trong \(\Delta AKI\) ta có:
\(\widehat {AIK} + \widehat {IKA} + \widehat {KAI} = {180^ \circ }\) (tổng ba góc trong một tam giác)
\( \Rightarrow \widehat {IAK} = {180^ \circ } - \widehat {AIK} - \widehat {AKI} = {180^ \circ } - {60^ \circ } - {50^ \circ } = {70^ \circ }\).
Áp dụng định lí sin vào \(\Delta AKI\), ta có:
\(\frac{{AK}}{{{\rm{sin}}\widehat {AIK}}} = \frac{{IK}}{{{\rm{sin}}\widehat {KAI}}} = \frac{{AI}}{{{\rm{sin}}\widehat {IKA}}}\)
\( \Rightarrow AK = \frac{{IK.{\rm{sin}}\widehat {AIK}}}{{{\rm{sin}}\widehat {KAI}}} = \frac{{380.{\rm{sin}}{{60}^ \circ }}}{{{\rm{sin}}{{70}^ \circ }}} \approx 350,21\left( {\rm{m}} \right)\).
Ta có \(\widehat {KAI} + \widehat {KAB} = {180^ \circ }\) (hai góc kề bù)
\(\widehat {KAB} = {180^ \circ } - \widehat {KAI} = {180^ \circ } - {70^ \circ } = {110^ \circ }\).
Áp dụng định lí sin vào \(\Delta AKB\), ta có:
\( \Rightarrow AB = \frac{{AK.{\rm{sin}}\widehat {AKB}}}{{{\rm{sin}}\widehat {ABK}}} = \frac{{350,21.{\rm{sin}}\left( {{{65}^ \circ } - {{50}^ \circ }} \right)}}{{{\rm{sin}}\left( {{{180}^ \circ } - {{110}^ \circ } - {{15}^ \circ }} \right)}} \approx 110,65\left( {\rm{m}} \right)\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án
1440 số.
Giải thích
Để lập số có số 2 và số 3 đứng cạnh nhau, ta ghép số 2 và 3 với nhau, đặt vào 1 vị trí.
Khi đó ta cần chọn các chữ số sắp xếp vào 5 vị trí để lập được số tự nhiên có 6 chữ số khác nhau.
+ Vị trí đầu tiên có 6 cách chọn: 1; 2 và \(3;4;5;6\).
+ Chọn 4 vị trí còn lại từ tập gồm \(0;1;2\) và \(3;4;5;6\) trừ đi số đã chọn vào vị trí đầu tiên \( \Rightarrow \) có \(A_5^4\) cách.
+ Mặt khác, có \(2! = 2\) cách sắp xếp vị trí cho chữ số 2 và 3.
Vậy có \(6.A_5^4.2 = 1440\) số thỏa mãn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án
31,4mV.
Giải thích
Suất điện động cảm ứng xuất hiện trong khung dây là
\({e_c} = N.\left| {\frac{{\Delta \Phi }}{{\Delta t}}} \right| = \left| {\frac{{\Delta B.S.\cos \alpha }}{{\Delta t}}} \right| = \left| {\frac{{{{10}^{ - 2}}.\pi .0,{1^2}.\cos {0^^\circ }}}{{0,01}}} \right| = \pi {.10^{ - 2}}V \approx 31,4\,\,mV\).
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
D. \(CD \approx 26,21{\rm{\;m}}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
B. Vua Lê Thái Tổ.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập