Một bể chứa nước có dạng hình cầu có phương trình là trong không gian Oxyz (đơn vị trên trục: m ). Bề mặt nước trong bể cách thành bể một khoảng lớn nhất là 50 cm. Khi đó bề mặt nước là hình tròn có đường kính là bao nhiêu mét? (Kết quả làm tròn đến chữ số thập phân thứ nhất)
Đáp án: ____
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án
1,7
Giải thích
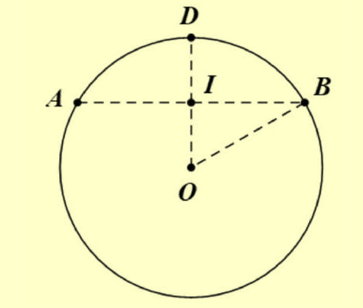
Ta có mặt cắt theo chiều dọc của bể như hình vẽ sau, trong đó \(O\) là tâm bể, \(D\) là đỉnh bể, \(AB\) là đường kính của bề mặt nước trong bể, I là trung điểm AB.
Đổi \(50\,\,cm = 0,5\,\,m\)
Bán kính bể là \(R = 1 = OD = OB\) mà \(DI = 0,5 = \frac{{OD}}{2},\,\,OD \bot AB \Rightarrow \Delta ODB\) đều cạnh bằng 1.
\( \Rightarrow BI = \frac{{\sqrt 3 }}{2} \Rightarrow AB = 2BI = \sqrt 3 \approx 1,7\left( m \right)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. providing
B. provide
C. provided
D. provides
Lời giải
Đáp án
providing
Giải thích
commit to V-ing: cam kết làm việc gì
Câu 2
A. hoàn thành cách mạng dân chủ nhân dân.
B. xóa bỏ chế độ quân chủ chuyên chế.
C. bắt đầu xây dựng chủ nghĩa xã hội.
D. đứng lên lật đổ chế độ tư sản – địa chủ.
Lời giải
Đáp án
hoàn thành cách mạng dân chủ nhân dân.
Giải thích
Giai đoạn 1945 – 1949, các nước Đông Âu hoàn thành cuộc cách mạng dân chủ nhân dân thông qua việc tiến hành cải cách ruộng đất, ban hành văn bản công nhận các quyền tự do dân chủ, cải thiện và nâng cao đời sống nhân dân. Tháng 10 – 1949, nước Cộng hòa Dân chủ Đức ra đời và sau đó tham gia vào hệ thống các nước xã hội chủ nghĩa Đông Âu. Như vậy, đáp án đúng là hoàn thành cách mạng dân chủ nhân dân.
Câu 3
A. amide -CO-NH- trong phân tử.
B. -CO- trong phân tử.
C. - NH- trong phân tử.
D. -CH(CN)-trong phân tử.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. The history of badminton and how it is played and organized. (1)
B. The badminton Olympics throughout the year. (2)
C. How to play badminton. (3)
D. The popularity of badminton in daily life and in international games. (4)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Đánh dấu sự sụp đổ hoàn toàn của đế quốc Nga và chính phủ tư sản.
B. Làm thất bại ý đồ chia rẽ liên minh của Nga Xô viết và đồng minh.
C. Chứng minh tính đúng đắn, khoa học của học thuyết Mác - Lê-nin.
D. Tạo sức mạnh tổng hợp để Liên Xô xây dựng và bảo vệ đất nước.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. chính trị.
B. tổ chức.
C. xã hội.
D. kinh tế.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. 414 kJ.
B. 567 kJ.
C. 4707 kJ.
D. 1395 kJ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập