Ông An muốn xây một bể nước dạng hình hộp chữ nhật có nắp với dung tích 3 mét khối. Đáy bể là một hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công để xây bể là 500000 đồng cho mỗi mét vuông. Hỏi chi phí thấp nhất ông An cần bỏ ra để xây bể nước là bao nhiêu?
Ông An muốn xây một bể nước dạng hình hộp chữ nhật có nắp với dung tích 3 mét khối. Đáy bể là một hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công để xây bể là 500000 đồng cho mỗi mét vuông. Hỏi chi phí thấp nhất ông An cần bỏ ra để xây bể nước là bao nhiêu?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án
6490123 đồng.
Giải thích
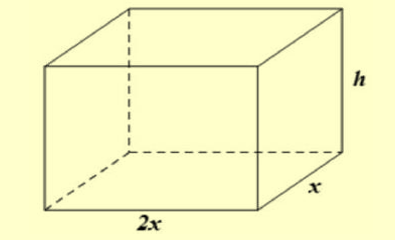
Gọi \(x\,\,(x > 0)\) là chiều rộng của đáy bể, suy ra chiều dài của đáy bể là \(2x\) và gọi \(h\) là chiều cao của bể. Diện tích xây dựng là diện tích toàn phần của bể \(S = 2.2xh + 2.xh + 2.2x.x = 4{x^2} + 6xh\) (1)
Ta có \(V = 3 = 2x.x.h \Rightarrow h = \frac{3}{{2{x^2}}}\,\,\left( 2 \right)\).
Thay \(\left( 2 \right)\) vào \(\left( 1 \right)\), ta được hàm \(S\left( x \right) = 4{x^2} + \frac{9}{x}\), với \(x > 0\)
Ta có \(S\left( x \right) = 4{x^2} + \frac{9}{x} = 4{x^2} + \frac{9}{{2x}} + \frac{9}{{2x}} \ge 3\sqrt[3]{{4{x^2}.\frac{9}{{2x}}.\frac{9}{{2x}}}} = 3\sqrt[3]{{81}}\).
Dấu "\( = \)" xảy ra khi và chỉ khi \(4{x^2} = \frac{9}{{2x}} \Leftrightarrow x = \frac{{\sqrt[3]{9}}}{2}\).
Khi đó chi phí thấp nhất là \(3\sqrt[3]{{81}} \times 500000 \approx 6490123\) (đồng).
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án
1440 số.
Giải thích
Để lập số có số 2 và số 3 đứng cạnh nhau, ta ghép số 2 và 3 với nhau, đặt vào 1 vị trí.
Khi đó ta cần chọn các chữ số sắp xếp vào 5 vị trí để lập được số tự nhiên có 6 chữ số khác nhau.
+ Vị trí đầu tiên có 6 cách chọn: 1; 2 và \(3;4;5;6\).
+ Chọn 4 vị trí còn lại từ tập gồm \(0;1;2\) và \(3;4;5;6\) trừ đi số đã chọn vào vị trí đầu tiên \( \Rightarrow \) có \(A_5^4\) cách.
+ Mặt khác, có \(2! = 2\) cách sắp xếp vị trí cho chữ số 2 và 3.
Vậy có \(6.A_5^4.2 = 1440\) số thỏa mãn.
Lời giải
Đáp án
31,4mV.
Giải thích
Suất điện động cảm ứng xuất hiện trong khung dây là
\({e_c} = N.\left| {\frac{{\Delta \Phi }}{{\Delta t}}} \right| = \left| {\frac{{\Delta B.S.\cos \alpha }}{{\Delta t}}} \right| = \left| {\frac{{{{10}^{ - 2}}.\pi .0,{1^2}.\cos {0^^\circ }}}{{0,01}}} \right| = \pi {.10^{ - 2}}V \approx 31,4\,\,mV\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
B. Vua Lê Thái Tổ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
D. \(CD \approx 26,21{\rm{\;m}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập