Cho hàm số bậc bốn y = f(x), hàm số y = f'(x) có bảng xét dấu như sau:
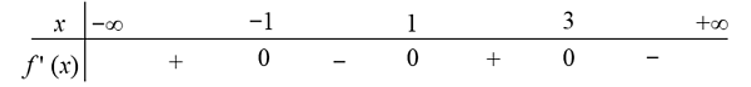
Hàm số có bao nhiêu điểm cực tiểu?
Đáp án: __
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án
1
Giải thích
Cách 1. Đặt \(g\left( x \right) = f\left( {\sqrt {{x^2} - 2x + 2} } \right)\) ta có:
\(g'\left( x \right) = f'\left( {\sqrt {{x^2} - 2x + 2} } \right).\frac{{2x - 2}}{{2\sqrt {{x^2} - 2x + 2} }} = f'\left( {\sqrt {{x^2} - 2x + 2} } \right).\frac{{x - 1}}{{\sqrt {{x^2} - 2x + 2} }}\)
Ta có:
\(g'(x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{f'(\sqrt {{x^2} - 2x + 2} ) = 0}\\{x - 1 = 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\sqrt {{x^2} - 2x + 2} = - 1}\\{\sqrt {{x^2} - 2x + 2} = 1}\\{\sqrt {{x^2} - 2x + 2} = 3}\\{x = 1}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{x^2} - 2x - 7 = 0}\\{x = 1}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1 - 2\sqrt 2 }\\{x = 1 + 2\sqrt 2 }\\{x = 1}\end{array}} \right.} \right.} \right.} \right.\)
Chú ý rằng khi \(x \to - \infty \) thì \(\sqrt {{x^2} - 2x + 2} \to + \infty \), nên khi \(x \to - \infty \) thì \(f'\left( {\sqrt {{x^2} - 2x + 2} } \right) < 0\), do đó \(g'\left( x \right) > 0\).
Từ đó ta có bảng xét dấu \(g'\left( x \right)\) như sau:
Từ đó hàm số \(g\left( x \right)\) có 3 điểm cực trị, trong đó có 1 điểm cực tiểu và 2 điểm cực đại.
Cách 2. Ghép trục
Đặt \(u = \sqrt {{x^2} - 2x + 2} \)
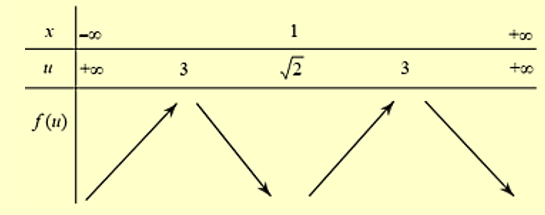
Vậy hàm số \(g\left( x \right)\) có 3 điểm cực trị, trong đó có 1 điểm cực tiểu và 2 điểm cực đại.
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án
1440 số.
Giải thích
Để lập số có số 2 và số 3 đứng cạnh nhau, ta ghép số 2 và 3 với nhau, đặt vào 1 vị trí.
Khi đó ta cần chọn các chữ số sắp xếp vào 5 vị trí để lập được số tự nhiên có 6 chữ số khác nhau.
+ Vị trí đầu tiên có 6 cách chọn: 1; 2 và \(3;4;5;6\).
+ Chọn 4 vị trí còn lại từ tập gồm \(0;1;2\) và \(3;4;5;6\) trừ đi số đã chọn vào vị trí đầu tiên \( \Rightarrow \) có \(A_5^4\) cách.
+ Mặt khác, có \(2! = 2\) cách sắp xếp vị trí cho chữ số 2 và 3.
Vậy có \(6.A_5^4.2 = 1440\) số thỏa mãn.
Lời giải
Đáp án
31,4mV.
Giải thích
Suất điện động cảm ứng xuất hiện trong khung dây là
\({e_c} = N.\left| {\frac{{\Delta \Phi }}{{\Delta t}}} \right| = \left| {\frac{{\Delta B.S.\cos \alpha }}{{\Delta t}}} \right| = \left| {\frac{{{{10}^{ - 2}}.\pi .0,{1^2}.\cos {0^^\circ }}}{{0,01}}} \right| = \pi {.10^{ - 2}}V \approx 31,4\,\,mV\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
B. Vua Lê Thái Tổ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
D. \(CD \approx 26,21{\rm{\;m}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập