Cho tam giác nhọn \(ABC\) không cân nội tiếp đường tròn tâm \(O.\) Vẽ đường kính \(AT\) của đường tròn \(\left( O \right)\) và lấy điểm \(P\) trên đoạn thẳng \(OT\,\,\left( {P \ne T} \right).\) Gọi \(E\) và \(F\) tương ứng là hình chiếu vuông góc của \(P\) trên các đường thẳng \(AC\) và \(AB.\) Gọi \(H\) là hình chiếu vuông góc của \(A\) trên cạnh \(BC.\)
a) Chứng minh \[\widehat {OAB}\, = \widehat {HAC}\] và hai đường thẳng \(BC,\,\,EF\) song song với nhau.
b) Cho \(AH\) và \[EF\]cắt nhau tại \(U;\) điểm \(Q\) di động trên đoạn thẳng \(UE\,\,\left( {Q \ne U,\,\,\,Q \ne E} \right).\)Đường thẳng vuông góc với AQ tại điểm Q cắt các đường thẳng \(PE,\,\,PF\) tương ứng tại \(M,\,\,N.\) Gọi \(K\) là tâm đường tròn ngoại tiếp tam giác \(AMN.\) Chứng minh bốn điểm \[A,\,\,M,\,\,N,\,\,P\] cùng thuộc một đường tròn và \(\widehat {OAH} = \widehat {KAQ}.\)
c) Kẻ \(KD\) vuông góc với \(BC\,\,\left( {D \in BC} \right).\) Chứng minh đường thẳng đi qua điểm \(D\) và song song với \(AQ\) luôn đi qua một điểm cố định.
Cho tam giác nhọn \(ABC\) không cân nội tiếp đường tròn tâm \(O.\) Vẽ đường kính \(AT\) của đường tròn \(\left( O \right)\) và lấy điểm \(P\) trên đoạn thẳng \(OT\,\,\left( {P \ne T} \right).\) Gọi \(E\) và \(F\) tương ứng là hình chiếu vuông góc của \(P\) trên các đường thẳng \(AC\) và \(AB.\) Gọi \(H\) là hình chiếu vuông góc của \(A\) trên cạnh \(BC.\)
a) Chứng minh \[\widehat {OAB}\, = \widehat {HAC}\] và hai đường thẳng \(BC,\,\,EF\) song song với nhau.
b) Cho \(AH\) và \[EF\]cắt nhau tại \(U;\) điểm \(Q\) di động trên đoạn thẳng \(UE\,\,\left( {Q \ne U,\,\,\,Q \ne E} \right).\)Đường thẳng vuông góc với AQ tại điểm Q cắt các đường thẳng \(PE,\,\,PF\) tương ứng tại \(M,\,\,N.\) Gọi \(K\) là tâm đường tròn ngoại tiếp tam giác \(AMN.\) Chứng minh bốn điểm \[A,\,\,M,\,\,N,\,\,P\] cùng thuộc một đường tròn và \(\widehat {OAH} = \widehat {KAQ}.\)
c) Kẻ \(KD\) vuông góc với \(BC\,\,\left( {D \in BC} \right).\) Chứng minh đường thẳng đi qua điểm \(D\) và song song với \(AQ\) luôn đi qua một điểm cố định.
Quảng cáo
Trả lời:
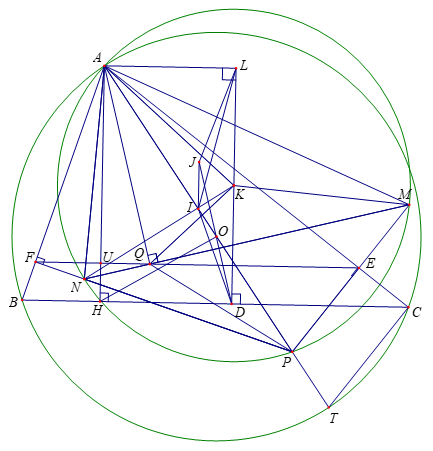
Ta có \(\widehat {BAH} = \widehat {OAC}\) do cùng phụ với \(\widehat {ABC}\), suy ra \[\widehat {PAF} = \widehat {HAC}\].
Có AEPF là tứ giác nội tiếp, suy ra \[\widehat {AEF} = \widehat {APF}\]
Có \[\widehat {APF} = {90^0} - \widehat {PAF}\] và \(\widehat {ACB} = {90^0} - \widehat {HAC}\)\[ \Rightarrow \widehat {AEF} = \widehat {ACB} \Rightarrow EF//BC\]
AQEM là tứ giác nội tiếp \[ \Rightarrow \widehat {AMN} = \widehat {AEF} = \widehat {APN} \Rightarrow \]\(A,M,N,P\) cùng nằm trên một đường tròn.
Ta có \(\widehat {AMN} = \widehat {ACB}\), tương tự \(\widehat {ANM} = \widehat {ABC}\)
\(\widehat {OAH} = \widehat {OAB} - \widehat {HAB} = {90^0} - \widehat {ACB} - \left( {{{90}^0} - \widehat {ABC}} \right)\)
\( = {90^0} - \widehat {AMN} - \left( {{{90}^0} - \widehat {ANM}} \right) = \widehat {KAN} - \widehat {QAN} = \widehat {KAQ}\)
Gọi \(L\) là chân đường vuông góc hạ từ điểm \(A\) xuống đường thẳng \(KD\).
Từ \(\widehat {OAH} = \widehat {KAQ} \Rightarrow \widehat {KAO} = \widehat {KAQ} - \widehat {OAQ} = \widehat {OAH} - \widehat {OAQ} = \widehat {QAH}\).
Gọi \(I\) là trung điểm của đoạn thẳng \(AP\) và J là giao điểm của đường thẳng qua D song song với AQ và đường thẳng qua I vuông góc với BC. \( \Rightarrow \widehat {QAH} = \widehat {JDL}\)
\( \Rightarrow \widehat {ILK} = \widehat {JDL}\), mặt khác ta có IJ//LD nên suy ra tứ giác ILDJ (hoặc IJLD) là hình thang cân.
Suy ra, I và J đối xứng với nhau qua trung trực của DL, hay qua trung trực của AH.Do ALDH là hình chữ nhật (dễ thấy). Từ đây, vì I là điểm cố định và trung trực của AH là đường thẳng cố định nên J là điểm cố định.
Không mất tính tổng quát, ta giả sử ab ≥ 0. Khi đó
\(P + 3 \ge \frac{{{{\left( {a + b + 2} \right)}^2}}}{{{{(a + b)}^2} + 4}} + \frac{{{{(c + 1)}^2}}}{{{c^2} + 2}} = \frac{{{{(c - 2)}^2}}}{{{c^2} + 4}} + \frac{{{{(c + 1)}^2}}}{{{c^2} + 2}}\).
Xét BĐT: \(\frac{{{{(c - 2)}^2}}}{{{c^2} + 4}} + \frac{{{{(c + 1)}^2}}}{{{c^2} + 2}} \ge \frac{3}{2} \Leftrightarrow {c^2}{\left( {c - 2} \right)^2} \ge 0\) (đúng).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a)Ta có \({(a - b)^2} = {4.5^m} - 20ab \vdots 5\)\[ \Rightarrow (a - b) \vdots 5 \Rightarrow {(a - b)^2} \vdots 25\].
\(a,b \ge 2 \Rightarrow {a^2} + {b^2} + 18ab = {4.5^m} \ge 80 \Rightarrow m \ge 2\)
\( \Rightarrow 20ab = {(a - b)^2} - {4.5^m} \vdots 25\)\( \Rightarrow 20ab \vdots 25 \Rightarrow ab \vdots 5\)
\( \Rightarrow \left[ \begin{array}{l}a \vdots 5\\b \vdots 5\end{array} \right.\)\( \Rightarrow \left\{ \begin{array}{l}a \vdots 5\\b \vdots 5\end{array} \right. \Rightarrow a = b = 5;m = 3.\)
b)Gọi \(X\) là tập 4 điểm được gán các số 1, 2, 3, 4 và \(Y\) là tập 4 điểm còn lại. Ta sẽ chỉ ra rằng tồn tại 4 dây cung không có điểm chung, mỗi dây cung nối một điểm của X và một điểm của Y. Một cách nối như vậy thoả mãn yêu cầu bài toán vì tổng các số tương ứng với 4 dây cung này bằng \(5 + 6 + 7 + 8 - 4 - 3 - 2 - 1 = 16\).
Dễ thấy rằng có một điểm của \(X\) nằm kề một điểm của \(Y\). Kẻ dây cung nối 2 điểm này rồi loại bỏ 2 điểm đánh dấu này lẫn dây cung đi, ta còn lại 6 điểm được đánh dấu trên đường tròn và 2 tập con \({X_1}\), \({Y_1}\) tương ứng, mỗi tập gồm 3 điểm được đánh dấu.
Bây giờ, lập luận tương tự, ta cũng suy ra có một điểm của \({X_1}\) kề nhau với một điểm \({Y_1}\) trên đường tròn đã bỏ đi 2 điểm trước đó. Kẻ dây cung nối 2 điểm này rồi loại bỏ 2 điểm đánh dấu này lẫn dây cung đi, ta còn lại 4 điểm được đánh dấu trên đường tròn và 2 tập con\({X_2},\)\({Y_2}\) tương ứng, mỗi tập gồm 2 điểm được đánh dấu.
Lập luận tương tự, ta cũng suy ra có một điểm của \({X_2}\) kề nhau với một điểm \({Y_2}\) trên đường tròn đã bỏ đi 2 điểm trước đó. Kẻ dây cung nối 2 điểm này cũng như dây cung nối 2 điểm còn lại. Bây giờ, khôi phục lại các dây cung ban đầu. Dễ thấy, 4 dây cung được kẻ đôi một không có điểm chung.
Lời giải
Không mất tính tổng quát, ta giả sử ab ≥ 0. Khi đó
\(P + 3 \ge \frac{{{{\left( {a + b + 2} \right)}^2}}}{{{{(a + b)}^2} + 4}} + \frac{{{{(c + 1)}^2}}}{{{c^2} + 2}} = \frac{{{{(c - 2)}^2}}}{{{c^2} + 4}} + \frac{{{{(c + 1)}^2}}}{{{c^2} + 2}}\).
Xét BĐT: \(\frac{{{{(c - 2)}^2}}}{{{c^2} + 4}} + \frac{{{{(c + 1)}^2}}}{{{c^2} + 2}} \ge \frac{3}{2} \Leftrightarrow {c^2}{\left( {c - 2} \right)^2} \ge 0\) (đúng).
Vậy \(P \ge \frac{{ - 3}}{2}\); dấu đẳng thức xảy ra chẳng hạn khi \(a = b = c = 0\), \(a = b = - 1,c = 2\). Do đó \[{P_{\min }} = \frac{{ - 3}}{2}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.