Cho các số thực \(a,\,\,b,\,\,c\) thoả mãn \(a + b + c = 0\). Tìm giá trị nhỏ nhất của biểu thức:
\(P = \frac{{2a - 1}}{{{a^2} + 2}} + \frac{{2b - 1}}{{{b^2} + 2}} + \frac{{2c - 1}}{{{c^2} + 2}} \cdot \)
Quảng cáo
Trả lời:
Không mất tính tổng quát, ta giả sử ab ≥ 0. Khi đó
\(P + 3 \ge \frac{{{{\left( {a + b + 2} \right)}^2}}}{{{{(a + b)}^2} + 4}} + \frac{{{{(c + 1)}^2}}}{{{c^2} + 2}} = \frac{{{{(c - 2)}^2}}}{{{c^2} + 4}} + \frac{{{{(c + 1)}^2}}}{{{c^2} + 2}}\).
Xét BĐT: \(\frac{{{{(c - 2)}^2}}}{{{c^2} + 4}} + \frac{{{{(c + 1)}^2}}}{{{c^2} + 2}} \ge \frac{3}{2} \Leftrightarrow {c^2}{\left( {c - 2} \right)^2} \ge 0\) (đúng).
Vậy \(P \ge \frac{{ - 3}}{2}\); dấu đẳng thức xảy ra chẳng hạn khi \(a = b = c = 0\), \(a = b = - 1,c = 2\). Do đó \[{P_{\min }} = \frac{{ - 3}}{2}\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
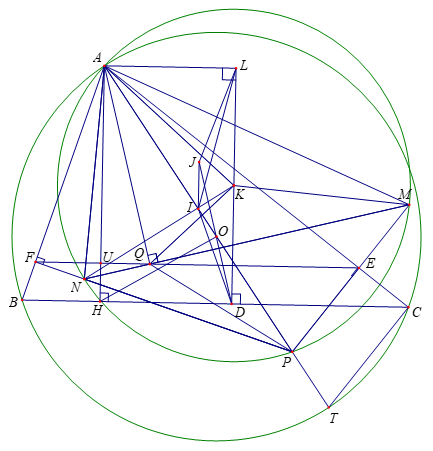
Ta có \(\widehat {BAH} = \widehat {OAC}\) do cùng phụ với \(\widehat {ABC}\), suy ra \[\widehat {PAF} = \widehat {HAC}\].
Có AEPF là tứ giác nội tiếp, suy ra \[\widehat {AEF} = \widehat {APF}\]
Có \[\widehat {APF} = {90^0} - \widehat {PAF}\] và \(\widehat {ACB} = {90^0} - \widehat {HAC}\)\[ \Rightarrow \widehat {AEF} = \widehat {ACB} \Rightarrow EF//BC\]
AQEM là tứ giác nội tiếp \[ \Rightarrow \widehat {AMN} = \widehat {AEF} = \widehat {APN} \Rightarrow \]\(A,M,N,P\) cùng nằm trên một đường tròn.
Ta có \(\widehat {AMN} = \widehat {ACB}\), tương tự \(\widehat {ANM} = \widehat {ABC}\)
\(\widehat {OAH} = \widehat {OAB} - \widehat {HAB} = {90^0} - \widehat {ACB} - \left( {{{90}^0} - \widehat {ABC}} \right)\)
\( = {90^0} - \widehat {AMN} - \left( {{{90}^0} - \widehat {ANM}} \right) = \widehat {KAN} - \widehat {QAN} = \widehat {KAQ}\)
Gọi \(L\) là chân đường vuông góc hạ từ điểm \(A\) xuống đường thẳng \(KD\).
Từ \(\widehat {OAH} = \widehat {KAQ} \Rightarrow \widehat {KAO} = \widehat {KAQ} - \widehat {OAQ} = \widehat {OAH} - \widehat {OAQ} = \widehat {QAH}\).
Gọi \(I\) là trung điểm của đoạn thẳng \(AP\) và J là giao điểm của đường thẳng qua D song song với AQ và đường thẳng qua I vuông góc với BC. \( \Rightarrow \widehat {QAH} = \widehat {JDL}\)
\( \Rightarrow \widehat {ILK} = \widehat {JDL}\), mặt khác ta có IJ//LD nên suy ra tứ giác ILDJ (hoặc IJLD) là hình thang cân.
Suy ra, I và J đối xứng với nhau qua trung trực của DL, hay qua trung trực của AH.Do ALDH là hình chữ nhật (dễ thấy). Từ đây, vì I là điểm cố định và trung trực của AH là đường thẳng cố định nên J là điểm cố định.
Không mất tính tổng quát, ta giả sử ab ≥ 0. Khi đó
\(P + 3 \ge \frac{{{{\left( {a + b + 2} \right)}^2}}}{{{{(a + b)}^2} + 4}} + \frac{{{{(c + 1)}^2}}}{{{c^2} + 2}} = \frac{{{{(c - 2)}^2}}}{{{c^2} + 4}} + \frac{{{{(c + 1)}^2}}}{{{c^2} + 2}}\).
Xét BĐT: \(\frac{{{{(c - 2)}^2}}}{{{c^2} + 4}} + \frac{{{{(c + 1)}^2}}}{{{c^2} + 2}} \ge \frac{3}{2} \Leftrightarrow {c^2}{\left( {c - 2} \right)^2} \ge 0\) (đúng).
Lời giải
a)Ta có \({(a - b)^2} = {4.5^m} - 20ab \vdots 5\)\[ \Rightarrow (a - b) \vdots 5 \Rightarrow {(a - b)^2} \vdots 25\].
\(a,b \ge 2 \Rightarrow {a^2} + {b^2} + 18ab = {4.5^m} \ge 80 \Rightarrow m \ge 2\)
\( \Rightarrow 20ab = {(a - b)^2} - {4.5^m} \vdots 25\)\( \Rightarrow 20ab \vdots 25 \Rightarrow ab \vdots 5\)
\( \Rightarrow \left[ \begin{array}{l}a \vdots 5\\b \vdots 5\end{array} \right.\)\( \Rightarrow \left\{ \begin{array}{l}a \vdots 5\\b \vdots 5\end{array} \right. \Rightarrow a = b = 5;m = 3.\)
b)Gọi \(X\) là tập 4 điểm được gán các số 1, 2, 3, 4 và \(Y\) là tập 4 điểm còn lại. Ta sẽ chỉ ra rằng tồn tại 4 dây cung không có điểm chung, mỗi dây cung nối một điểm của X và một điểm của Y. Một cách nối như vậy thoả mãn yêu cầu bài toán vì tổng các số tương ứng với 4 dây cung này bằng \(5 + 6 + 7 + 8 - 4 - 3 - 2 - 1 = 16\).
Dễ thấy rằng có một điểm của \(X\) nằm kề một điểm của \(Y\). Kẻ dây cung nối 2 điểm này rồi loại bỏ 2 điểm đánh dấu này lẫn dây cung đi, ta còn lại 6 điểm được đánh dấu trên đường tròn và 2 tập con \({X_1}\), \({Y_1}\) tương ứng, mỗi tập gồm 3 điểm được đánh dấu.
Bây giờ, lập luận tương tự, ta cũng suy ra có một điểm của \({X_1}\) kề nhau với một điểm \({Y_1}\) trên đường tròn đã bỏ đi 2 điểm trước đó. Kẻ dây cung nối 2 điểm này rồi loại bỏ 2 điểm đánh dấu này lẫn dây cung đi, ta còn lại 4 điểm được đánh dấu trên đường tròn và 2 tập con\({X_2},\)\({Y_2}\) tương ứng, mỗi tập gồm 2 điểm được đánh dấu.
Lập luận tương tự, ta cũng suy ra có một điểm của \({X_2}\) kề nhau với một điểm \({Y_2}\) trên đường tròn đã bỏ đi 2 điểm trước đó. Kẻ dây cung nối 2 điểm này cũng như dây cung nối 2 điểm còn lại. Bây giờ, khôi phục lại các dây cung ban đầu. Dễ thấy, 4 dây cung được kẻ đôi một không có điểm chung.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.