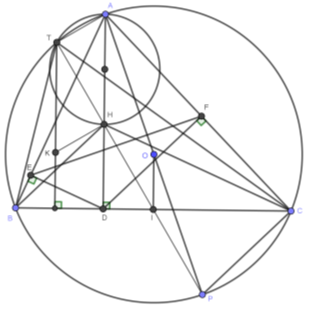
Cho tam giác \(ABC\) nhọn \(\left( {AB < AC} \right)\) nội tiếp đường tròn tâm \(O\), \(AD\) là đường cao. Gọi \(E\), \(F\) lần lượt là hình chiếu của \(D\) trên \(AB\), \(AC\). Gọi \(AP\) là đường kính của đường tròn \(\left( O \right)\).
1) Chứng minh tứ giác \(AEDF\) nội tiếp và \(AE.AB = AF.AC\).
2) Chứng minh tam giác \(ABC\) đồng dạng với tam giác \(AFE\) và \(AP\) vuông góc với \(EF\).
3) Gọi \(H\) là trực tâm của tam giác \(ABC\). Đường tròn đường kính \(AH\) cắt đường tròn \(\left( O \right)\) tại điểm thứ hai \(T\). Gọi \(K\) là trực tâm của tam giác \(BTC\). Chứng minh tứ giác \(AHKT\) là hình bình hành.
Cho tam giác \(ABC\) nhọn \(\left( {AB < AC} \right)\) nội tiếp đường tròn tâm \(O\), \(AD\) là đường cao. Gọi \(E\), \(F\) lần lượt là hình chiếu của \(D\) trên \(AB\), \(AC\). Gọi \(AP\) là đường kính của đường tròn \(\left( O \right)\).
1) Chứng minh tứ giác \(AEDF\) nội tiếp và \(AE.AB = AF.AC\).
2) Chứng minh tam giác \(ABC\) đồng dạng với tam giác \(AFE\) và \(AP\) vuông góc với \(EF\).
3) Gọi \(H\) là trực tâm của tam giác \(ABC\). Đường tròn đường kính \(AH\) cắt đường tròn \(\left( O \right)\) tại điểm thứ hai \(T\). Gọi \(K\) là trực tâm của tam giác \(BTC\). Chứng minh tứ giác \(AHKT\) là hình bình hành.
Quảng cáo
Trả lời:
Giải bởi Vietjack
|
1)Ta có \(\widehat {AED} = 90^\circ \), \(\widehat {AFD} = 90^\circ \) |
|
Xét tứ giác \(AEDF\) có \(\widehat {AED} + \widehat {AFD} = 90^\circ + 90^\circ = 180^\circ \) suy ra tứ giác \(AEDF\) nội tiếp. |
|
Trong tam giác vuông \(ABD\) có \(DE\) là đường cao suy ra \(AE.AB = A{D^2}\,\,\,\left( 1 \right)\). |
|
Trong tam giác vuông \(ACD\) có \(DF\) là đường cao suy ra \(AF.AC = A{D^2}\,\,\,\left( 2 \right)\). Từ (1) và (2) ta có \(AE.AB = AF.AC\). |
|
2)Do \(AE.AB = AF.AC \Rightarrow \frac{{AB}}{{AF}} = \frac{{AC}}{{AE}}\), mà \(\widehat {BAC}\) chung Suy ra |
|
\( \Rightarrow \widehat {AEF} = \widehat {ACB}\) |
|
Ta có \(\widehat {BAP} = \widehat {BCP}\) |
|
Suy ra \(\widehat {AEF} + \widehat {BAP} = \widehat {ACB} + \widehat {BCP} = \widehat {ACP} = 90^\circ \) Vậy \(AP\) vuông góc với \(EF\). |
|
3)Ta có \(AH \bot BC\), \(TK \bot BC \Rightarrow AH\parallel TK\). |
|
Do \(BH \bot AC\), \(PC \bot AC \Rightarrow BH\parallel PC\). Do \(CH \bot AB\), \(PB \bot AB \Rightarrow CH\parallel PB\). Suy ra tứ giác \(BHCP\) là hình bình hành. Gọi \(I\) là trung điểm \(BC\), ta có \(OI = \frac{1}{2}AH\). |
|
Tương tự \(OI = \frac{1}{2}TK\). |
|
\( \Rightarrow AH = TK\). Vậy tứ giác \(AHKT\) là hình bình hành. |
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
1. a)Với \(m = 0\), phương trình \(\left( 1 \right)\) trở thành \({x^2} - x - 2 = 0\) |
|
\( \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 2\end{array} \right.\). |
|
b) Ta có \(\Delta = {\left( {2m + 1} \right)^2} - 4\left( {4m - 2} \right) = 4{m^2} - 12m + 9 = {\left( {2m - 3} \right)^2} \ge 0\,\,\forall m\). |
|
Áp dụng Viet \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m + 1\\{x_1}{x_2} = 4m - 2\end{array} \right.\) |
|
Ta có \(x_1^2 + x_2^2 = 13 \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = 13 \Leftrightarrow {\left( {2m + 1} \right)^2} - 2\left( {4m - 2} \right) = 13 \Leftrightarrow {m^2} - m - 2 = 0\) |
|
\( \Leftrightarrow \left[ \begin{array}{l}m = - 1\,\left( {tm} \right)\\m = 2\,\left( {tm} \right)\end{array} \right.\). Vậy \(m = - 1\), \(m = 2\). |
|
2) Điều kiện: \( - 1 \le x \le 4\). |
|
Phương trình trở thành \( \Leftrightarrow x + 1 + 2\sqrt {\left( {x + 1} \right)\left( {4 - x} \right)} + 4 - x = 2x + 9 \Leftrightarrow \sqrt {\left( {x + 1} \right)\left( {4 - x} \right)} = x + 2\) |
|
\( \Leftrightarrow \left\{ \begin{array}{l}x \ge - 2\\ - {x^2} + 3x + 4 = {x^2} + 4x + 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 2\\2{x^2} + x = 0\end{array} \right.\) |
|
\( \Leftrightarrow \left[ \begin{array}{l}x = 0\,\left( {tm} \right)\\x = - \frac{1}{2}\,\left( {tm} \right)\end{array} \right.\). Vậy nghiệm của phương trình là \(x = - \frac{1}{2}\), \(x = 0\). |
Lời giải
|
1)\[P = \sqrt {{{\left( {\sqrt {2023} + 1} \right)}^2}} - \sqrt {{{\left( {\sqrt {2024} + 1} \right)}^2}} \] |
|
\[ = \sqrt {2023} + 1 - \left( {\sqrt {2024} + 1} \right) = \sqrt {2023} - \sqrt {2024} \]. |
|
2)Tọa độ giao điểm là \(M\left( { - 1;0} \right)\). |
|
3)Gọi \(R\) là bán kính của đường tròn ngoại tiếp. Từ giả thiết ta có \(2R = 2\sqrt 2 \Leftrightarrow R = \sqrt 2 \). |
|
Vậy diện tích của hình tròn là \(S = \pi {R^2} = 2\pi \,\left( {c{m^2}} \right)\). |
|
4)Thể tích của hình nón là \(V = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi {.6^2}.8 = 96\pi \,\left( {c{m^3}} \right)\). |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập