a)  Giải phương trình \({x^4} - 4{x^3} + 6{x^2} - 4x - 3 = 0\)

b)  Giải hệ phương trình \(\left\{ \begin{array}{l}2x - \sqrt {x + y}  = \sqrt {2y - {x^2} + 2x} \\\left( {2 - \sqrt {x + y} } \right)\sqrt {{x^2} + 4}  = 2\sqrt 3 x\end{array} \right.\)

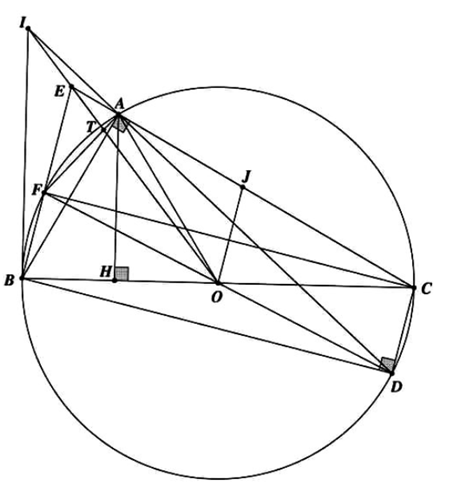
a) Vì tứ giác AFBC nội tiếp, ta có đẳng thức sau

\(180^\circ \, - \,\widehat {FAJ}\, = \,\widehat {EAF} = \,\widehat {FBC}\,\, = \,\frac{1}{2}\widehat {FOC}\,\)

Vì JO là đường trung bình tam giác CBE nên JO // BF mà \(CF\, \bot \,BF\) suy ra \(JO\, \bot \,BF\)

 Vì O thuộc trung trực CF nên OJ là trung trực CF nên

\(\widehat {FOJ}\, = \,\frac{1}{2}\widehat {FOC}\, = \,180^\circ \, - \,\widehat {FAJ}\)

Từ đây ta có ngay tứ giác AJOF là tứ giác nội tiếp

b) Gọi T là giao điểm của OE và AF. Trước hết, ta chỉ ra \(\frac{{ID}}{{IA}} = \frac{{B{D^2}}}{{B{A^2}}}\)

Thật vậy, áp dụng định lý Menelaus cho tam giác AFD, cát tuyến ITO ta có

\(\frac{{ID}}{{IA}}.\frac{{TA}}{{TF}}.\frac{{OF}}{{OD}} = 1\)

Từ đây kết hợp OF = OD, \(\Delta AEB\,\, \sim \,\,\Delta FEC\left( {g.g} \right)\) và BD = CF, ta có

\(\frac{{ID}}{{IA}} = \frac{{TF}}{{TA}} = \frac{{EF.\sin FET}}{{EA.\sin AET}} = \frac{{EF}}{{EA}}.\frac{{\sin BEO}}{{\sin CEO}} = \frac{{EF}}{{EA}}.\frac{{CE}}{{BE}} = {\left( {\frac{{CF}}{{BA}}} \right)^2} = {\left( {\frac{{BD}}{{BA}}} \right)^2}\)

Bằng các phép biến đổi góc, ta được

\[\widehat {OFA\,}\,\, = \,\,\widehat {OAF}\,\, = \,\,90^\circ \,\, - \,\,\widehat {ADF}\,\, = \,\,90^\circ \,\, - \,\,\widehat {ACF}\,\, = \,\,\widehat {AEF}\]

Do đó OF và OA là hai tiếp tuyến của đường tròn (AEF)

Gọi I’ là giao điểm của tiếp tuyến tại B của (O) với AD, ta có

\[\Delta I'BA\,\, \sim \,\,\Delta I'DB\left( {g.g} \right) \Rightarrow \frac{{I'A}}{{I'B}} = \frac{{I'B}}{{I'D}} = \frac{{BA}}{{BD}}\]

\[ \Leftrightarrow \frac{{I'D}}{{I'A}} = \frac{{I'D}}{{I'B}}.\frac{{I'B}}{{I'A}} = \frac{{B{D^2}}}{{B{A^2}}} = \frac{{ID}}{{IA}}\]

\[ \Rightarrow I \equiv I'\]

Từ đây ta được IB là tiếp tuyến của (O) suy ra \[\widehat {IBA}\,\, = \,\,\widehat {BDA}\]

Bài toán được chứng minh

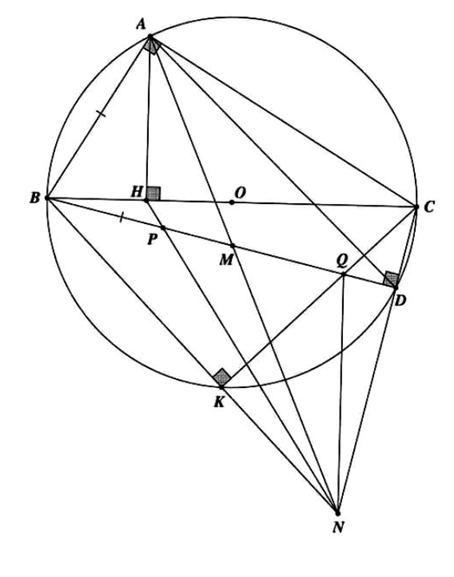
c) Ta có

\[\widehat {DNM}\,\, + \,\,\widehat {DMN}\,\, = \,\,\widehat {BAM}\,\, + \,\,\widehat {CAN}\,\, = \,\,90^\circ ,\,\widehat {BAM}\,\, = \,\,\widehat {BMA}\]

Do đó \[\widehat {CAN}\,\, = \,\,\widehat {CNA}\] hay tam giác CAN cân tại C suy ra CA = CN

Theo hệ thức lượng ta có \[C{A^2} = CH.CB\,\] nên \[C{N^2} = CH.CB\] suy ra \[\frac{{CN}}{{CH}} = \frac{{CB}}{{CN}}\]

Từ đây ta được \[\Delta CNH\,\, \sim \,\,\Delta CBN\left( {c.g.c} \right)\] dẫn đến \[\widehat {CHN}\, = \,\widehat {CNB}\, = \,\widehat {CQD}\]

Do đó tứ giác CQPH nội tiếp, ta có các biến đổi sau

\[BP.BQ\,\, = BH.BC\, = \,B{A^2} \Leftrightarrow B{M^2}\, = \,BP.BQ\]

\[ \Leftrightarrow \frac{{BM}}{{BP}}\, = \,\frac{{BQ}}{{BM}}\]

\[ \Leftrightarrow \frac{{PM}}{{BP}}\, = \,\frac{{MQ}}{{BQ}}\]

\[ \Leftrightarrow PM.BQ\, = \,MQ.BM\]

\[ \Leftrightarrow \left( {MB + MQ} \right)MP\, = \,MQ.MB\]

\[ \Leftrightarrow \frac{{MB + MQ}}{{MB.MQ}} = \frac{1}{{MP}}\]

\[ \Leftrightarrow \frac{1}{{MP}}\, = \,\frac{1}{{MQ}} + \frac{1}{{MB}}\]

Vậy bài toán được chứng minh