Cho một đa giác lồi có diện tích \(2024c{m^2}\). Chứng minh rằng bao giờ cũng vẽ được trong đa giác đó một tam giác có diện tích không nhỏ hơn \(759c{m^2}\)
Cho một đa giác lồi có diện tích \(2024c{m^2}\). Chứng minh rằng bao giờ cũng vẽ được trong đa giác đó một tam giác có diện tích không nhỏ hơn \(759c{m^2}\)
Quảng cáo
Trả lời:
Bài toán ta cần giải quyết tương đương bài toán tổng quát sau
Cho một đa giác lồi có diện tích bằng S. Chứng minh rằng bao giờ cũng vẽ được trong đa giác đó một tam giác lồi có diện tích không nhỏ hơn \[\frac{3}{8}S\]
Gọi a là đường thẳng chứa cạnh AB của đa giác. Gọi C là đỉnh của đa giác cách xa AB nhất. Qua C kẻ đường thẳng b//a
Kẻ đường thẳng d song song cách đều a và b, kẻ đường thẳng \[{d_1}\] song song cách đều a và d, kẻ đường thẳng \[{d_2}\] song song cách đều b và d. Gọi h là khoảng cách giữa a và b
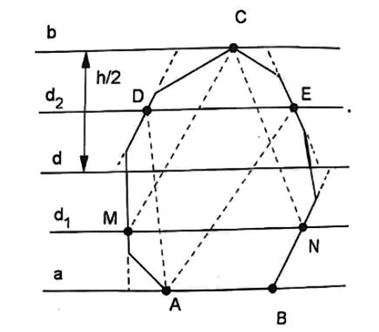
Gọi giao điểm của \[{d_1}\] với biên của đa giác là M và N. Kéo dài các cạnh của đa giác chứa M và N cho cắt a và d, ta được một hình thang có diện tích bằng \[MN.\frac{h}{2}\]
Gọi giao điểm của \[{d_2}\]với biên của đa giác là D và E. Kéo dài các cạnh của đa giác chứa D và E cho cắt b và d, ta được một hình thang ( cũng có thể làm tam giác ) có diện tích bằng \[DE.\frac{h}{2}\]
Hai hình thang nói trên phủ toàn bộ đa giác nên tổng các diện tích của hai hình thang lớn hơn hoặc bằng S, do đó: \[\left( {MN + DE} \right).\frac{h}{2}\, \ge S\]
Ta sẽ chứng minh rằng một trong hai tam giác ADE và CMN là tam giác phải tìm. Xét tổng diện tích hai tam giác đó:
\[{S_{ADE}} + {S_{CMN}} = \frac{1}{2}DE.\frac{{3h}}{4} + \frac{1}{2}MN.\frac{{3h}}{4} = \frac{{3h}}{8}\left( {DE + MN} \right)\]
\[ = \frac{3}{4}.\frac{h}{2}\left( {DE + MN} \right) \ge \frac{3}{4}S\]
Tồn tại một trong hai tam giác ADE, CMN có diện tích lớn hơn hoặc bằng \[\frac{3}{8}S\] đó là tam giác cần tìm. Vậy bài toán được chứng minh
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
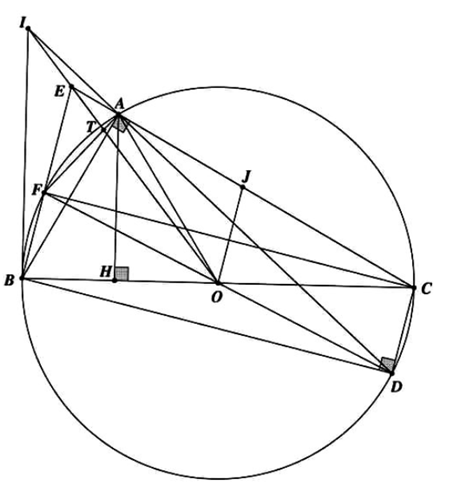
a) Vì tứ giác AFBC nội tiếp, ta có đẳng thức sau
\(180^\circ \, - \,\widehat {FAJ}\, = \,\widehat {EAF} = \,\widehat {FBC}\,\, = \,\frac{1}{2}\widehat {FOC}\,\)
Vì JO là đường trung bình tam giác CBE nên JO // BF mà \(CF\, \bot \,BF\) suy ra \(JO\, \bot \,BF\)
Vì O thuộc trung trực CF nên OJ là trung trực CF nên
\(\widehat {FOJ}\, = \,\frac{1}{2}\widehat {FOC}\, = \,180^\circ \, - \,\widehat {FAJ}\)
Từ đây ta có ngay tứ giác AJOF là tứ giác nội tiếp
b) Gọi T là giao điểm của OE và AF. Trước hết, ta chỉ ra \(\frac{{ID}}{{IA}} = \frac{{B{D^2}}}{{B{A^2}}}\)
Thật vậy, áp dụng định lý Menelaus cho tam giác AFD, cát tuyến ITO ta có
\(\frac{{ID}}{{IA}}.\frac{{TA}}{{TF}}.\frac{{OF}}{{OD}} = 1\)
Từ đây kết hợp OF = OD, \(\Delta AEB\,\, \sim \,\,\Delta FEC\left( {g.g} \right)\) và BD = CF, ta có
\(\frac{{ID}}{{IA}} = \frac{{TF}}{{TA}} = \frac{{EF.\sin FET}}{{EA.\sin AET}} = \frac{{EF}}{{EA}}.\frac{{\sin BEO}}{{\sin CEO}} = \frac{{EF}}{{EA}}.\frac{{CE}}{{BE}} = {\left( {\frac{{CF}}{{BA}}} \right)^2} = {\left( {\frac{{BD}}{{BA}}} \right)^2}\)
Bằng các phép biến đổi góc, ta được
\[\widehat {OFA\,}\,\, = \,\,\widehat {OAF}\,\, = \,\,90^\circ \,\, - \,\,\widehat {ADF}\,\, = \,\,90^\circ \,\, - \,\,\widehat {ACF}\,\, = \,\,\widehat {AEF}\]
Do đó OF và OA là hai tiếp tuyến của đường tròn (AEF)
Gọi I’ là giao điểm của tiếp tuyến tại B của (O) với AD, ta có
\[\Delta I'BA\,\, \sim \,\,\Delta I'DB\left( {g.g} \right) \Rightarrow \frac{{I'A}}{{I'B}} = \frac{{I'B}}{{I'D}} = \frac{{BA}}{{BD}}\]
\[ \Leftrightarrow \frac{{I'D}}{{I'A}} = \frac{{I'D}}{{I'B}}.\frac{{I'B}}{{I'A}} = \frac{{B{D^2}}}{{B{A^2}}} = \frac{{ID}}{{IA}}\]
\[ \Rightarrow I \equiv I'\]
Từ đây ta được IB là tiếp tuyến của (O) suy ra \[\widehat {IBA}\,\, = \,\,\widehat {BDA}\]
Bài toán được chứng minh
c) Ta có
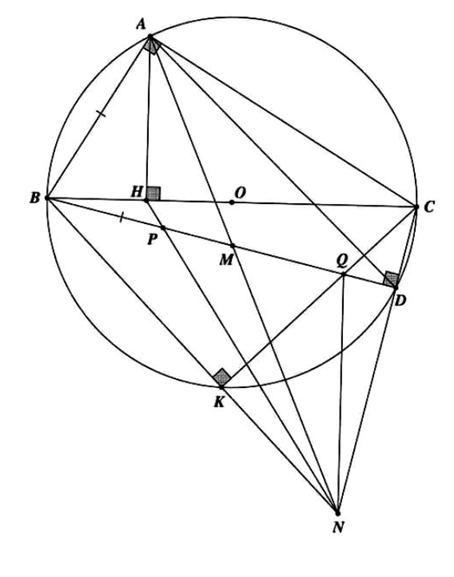
\[\widehat {DNM}\,\, + \,\,\widehat {DMN}\,\, = \,\,\widehat {BAM}\,\, + \,\,\widehat {CAN}\,\, = \,\,90^\circ ,\,\widehat {BAM}\,\, = \,\,\widehat {BMA}\]
Do đó \[\widehat {CAN}\,\, = \,\,\widehat {CNA}\] hay tam giác CAN cân tại C suy ra CA = CN
Theo hệ thức lượng ta có \[C{A^2} = CH.CB\,\] nên \[C{N^2} = CH.CB\] suy ra \[\frac{{CN}}{{CH}} = \frac{{CB}}{{CN}}\]
Từ đây ta được \[\Delta CNH\,\, \sim \,\,\Delta CBN\left( {c.g.c} \right)\] dẫn đến \[\widehat {CHN}\, = \,\widehat {CNB}\, = \,\widehat {CQD}\]
Do đó tứ giác CQPH nội tiếp, ta có các biến đổi sau
\[BP.BQ\,\, = BH.BC\, = \,B{A^2} \Leftrightarrow B{M^2}\, = \,BP.BQ\]
\[ \Leftrightarrow \frac{{BM}}{{BP}}\, = \,\frac{{BQ}}{{BM}}\]
\[ \Leftrightarrow \frac{{PM}}{{BP}}\, = \,\frac{{MQ}}{{BQ}}\]
\[ \Leftrightarrow PM.BQ\, = \,MQ.BM\]
\[ \Leftrightarrow \left( {MB + MQ} \right)MP\, = \,MQ.MB\]
\[ \Leftrightarrow \frac{{MB + MQ}}{{MB.MQ}} = \frac{1}{{MP}}\]
\[ \Leftrightarrow \frac{1}{{MP}}\, = \,\frac{1}{{MQ}} + \frac{1}{{MB}}\]
Vậy bài toán được chứng minh
Lời giải
a) Theo giả thiết ta có thể đặt như sau \(x + \sqrt {2024} = a,\,\frac{1}{x} - \sqrt {2024} = b\) thì \(a,b \in \mathbb{Z}\)
Bằng các phép biến đổi ta được
\(\left( {a - \sqrt {2024} } \right)\left( {b + \sqrt {2024} } \right) = 1 \Leftrightarrow \sqrt {2024} \left( {a - b} \right) = 2025 - ab\)
Vì \(\sqrt {2024} \) vô tỷ và a – b, 2025 – ab nguyên nên a = b và 2025 = ab suy ra \(a = b = \pm 45\)
Khi đó bằng phép thế ta được
\(x + \sqrt {2024} = a = \pm 45 \Leftrightarrow x \in \left\{ {45 - \sqrt {2024} ,\, - 45 - \sqrt {2024} } \right\}\)
Vậy tất cả giá trị x thỏa mãn là \(x \in \left\{ {45 - \sqrt {2024} ,\, - 45 - \sqrt {2024} } \right\}\)
b) Theo giả thiết \(2a = {b^3}\,\left( 1 \right)\) và \(5a = {c^2}\,\left( 2 \right)\) với b,c là các số nguyên dương.
Từ (1) suy ra \({b^3}\) chia hết cho 2, mà 2 là số nguyên tố nên b chia hết cho 2.
Đặt b = 2d, thay vào (1) được \(2a = 8{d^3}\), hay là \(a = 4{d^3}\,\left( 3 \right)\).
Từ (2) suy ra \({c^2}\) chia hết cho 5, mà 5 là số nguyên tố nên c chia hết cho 5
Đặt c = 5e, thay vào (2) được \(5a = 25{e^2}\), hay là \(a = 5{e^2}\,\left( 4 \right)\)
Từ (3) và (4) có \(a = 4{d^3} = 5{e^2}\,\left( 5 \right)\) với d,e là các số nguyên dương. Do 4 và 5 là hai số nguyên tố cùng nhau nên từ (5) thì \({d^3}\) chia hết cho 5, suy ra d chia hết cho 5
Đặt d = 5k, thay vào (5) được \(a = 5{e^2} = 500{k^3}\) với k là số nguyên dương
Từ đó \({e^2} = 100{k^3} = {10^2}{k^3}\). Điều này xảy ra với số k nhỏ nhất là k = 1, e = 10 và a = 500
Lúc đó \(2a = 1000 = {10^3}\) và \(5a = 2500 = {50^2}\) thỏa mãn bài toán
Vậy số nguyên dương a nhỏ nhất thỏa mãn là a – 500
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.