Cho đường tròn \(\left( O \right)\) đường kính \(AB\). Đường thẳng \(\Delta \) tiếp xúc với \(\left( O \right)\) tại \(A\), \(I\) là điểm cố định trên đoạn \(AB\)và \(CD\)là dây cung thay đổi của \(\left( O \right)\) luôn đi qua \(I\). Các đường thẳng \(BC,BD\) cắt \(\Delta \) lần lượt tại \(M,N\).
a) Chứng minh rằng \(CDMN\) là tứ giác nội tiếp.
b) Gọi \(K\)là giao điểm thứ hai của đường tròn ngoại tiếp tam giác \(BMN\) với đường thẳng \(AB\). Chứng minh rằng \(KMCI\) là tứ giác nội tiếp và tích \(AM.AN\)không đổi.
c) Gọi \(T\)là tâm đường tròn ngoại tiếp tứ giác \(CDNM\). Tìm vị trí của \(CD\) sao cho độ dài đoạn thẳng \(BT\)nhỏ nhất.
Cho đường tròn \(\left( O \right)\) đường kính \(AB\). Đường thẳng \(\Delta \) tiếp xúc với \(\left( O \right)\) tại \(A\), \(I\) là điểm cố định trên đoạn \(AB\)và \(CD\)là dây cung thay đổi của \(\left( O \right)\) luôn đi qua \(I\). Các đường thẳng \(BC,BD\) cắt \(\Delta \) lần lượt tại \(M,N\).
a) Chứng minh rằng \(CDMN\) là tứ giác nội tiếp.
b) Gọi \(K\)là giao điểm thứ hai của đường tròn ngoại tiếp tam giác \(BMN\) với đường thẳng \(AB\). Chứng minh rằng \(KMCI\) là tứ giác nội tiếp và tích \(AM.AN\)không đổi.
c) Gọi \(T\)là tâm đường tròn ngoại tiếp tứ giác \(CDNM\). Tìm vị trí của \(CD\) sao cho độ dài đoạn thẳng \(BT\)nhỏ nhất.
Quảng cáo
Trả lời:
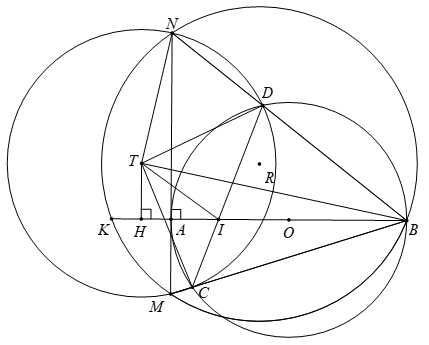
a) Áp dụng hệ thức lượng cho hai tam giác \[BAM\] và \[BAN\] với hai đường cao tương ứng là \[AC,AD\] ta có \[B{A^2} = BC.BM = BD.BN\]. Vì vậy tứ giác \[CDNM\] nội tiếp.
b) Ta có biến đổi góc \[\widehat {MKB} = \widehat {MNB} = \widehat {DCB}\], vì vậy tứ giác \[CIKM\] nội tiếp.
Do đó \[BC.BM = BI.BK = B{A^2}\], từ đây suy ra \[K\] là điểm cố định.
Từ đây ta suy ra \[AM.AN = AK.AB\] cố định.
c) Gọi \[r\] là bán kính của \[\left( T \right)\] thì \[{r^2} - T{A^2} = AN.AM = a\] không đổi. Ta cũng có \[ID.IC\] không đổi, đặt \[b = ID.IC = {r^2} - T{I^2}\] suy ra \[T{I^2} - T{A^2} = a - b\].
Gọi \[H\] là hình chiếu của \[K\]lên \[AB\] theo định lý Pythagore ta có.
\[\left( {AI + 2AH} \right).AI = H{I^2} - H{A^2}\]\[ = \left( {T{I^2} - T{H^2}} \right) - \left( {T{A^2} - T{H^2}} \right)\]\[ = T{I^2} - T{A^2} = a - b\]
Từ đây kết hợp với \[AI\] không đổi (\[A\] và \[I\] cố định) suy ra \[H\] cố định do đó \[BH\]không đổi.
Khi đó, theo định lý Pytagore ta có.
\[B{T^2} = T{H^2} + B{H^2} \ge B{H^2}.\]
Dấu bằng xảy ra khi và chỉ khi \[T\] trùng với \[H\] tức là \[BA\]là trung trực của \[CD\] suy ra \[CD\] vuông góc \[AB\] tại \[I\]. Vậy khi \[CD\] vuông góc với \[AB\] tại \[I\] thì độ dài đoạn thẳng \[BT\] nhỏ nhất.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Ta biến đổi phương trình như sau
\({x^2} - {y^2} + 2\left( {3x + y} \right) = 23\)\( \Leftrightarrow \left( {{x^2} + 6x + 9} \right) - \left( {{y^2} - 2y + 1} \right) = 31\)\( \Leftrightarrow {\left( {x + 3} \right)^2} - {\left( {y - 1} \right)^2} = 31\)\( \Leftrightarrow \left( {x - y + 4} \right)\left( {x + y + 2} \right) = 31\)
Từ đây, ta xét bảng sau \[\]
|
\[x - y + 4\] |
31 |
1 |
\[ - 31\] |
\[ - 1\] |
|
\[x + y + 2\] |
1 |
31 |
\[ - 1\] |
\[ - 31\] |
|
\[x\] |
13 |
13 |
\[ - 19\] |
\[ - 19\] |
|
\[y\] |
\[ - 14\] |
16 |
16 |
\[ - 14\] |
Vậy tất cả các nghiệm \[\left( {x,y} \right)\]thỏa mãn là \[\left( {13, - 14} \right);\left( {13,16} \right);\left( { - 19,16} \right);\left( { - 19, - 14} \right)\].
b) Gọi hai nghiệm nguyên của \(P\left( x \right) = {x^2} + bx + c\) là \[u,v\].
Theo định lý Vi – et ta được \[u + v = - b\], \[uv = c\].
Vì \[\left| {P\left( 9 \right)} \right|\] là số nguyên tố nên \[\left| {\left( {9 - u} \right)\left( {9 - v} \right)} \right|\] là số nguyên tố dẫn đến \[\left| {9 - u} \right| = 1\] hoặc \[\left| {9 - v} \right| = 1\].
Không mất tính tổng quát, ta giả sử \[\left| {9 - u} \right| = 1 \Leftrightarrow u \in \left\{ {8;10} \right\}\].
Trường hợp 1. \[u = 10\], vì \[\left| c \right| \le 16\], nên \[\left| v \right| \in \left\{ {0;1} \right\}\]\[ \Leftrightarrow v \in \left\{ { - 1;0;1} \right\}\].
Mặt khác \[9 - 1 = 8,\]\[9 - 0 = 9,\]\[9 + 1 = 10\] đều không là số nguyên tố nên trường hợp này loại.
Trường hợp 2. \[u = 8\], vì \[\left| c \right| \le 16\], nên \[\left| v \right| \le 2\].
Mà \[v\] phải là số chẵn nên từ đây suy ra \[v \in \left\{ { - 2;2} \right\}\]. Thử lại cả hai giá trị này thỏa mãn và ta nhận được giá trị của \[b,c\] tương ứng là \[ - 10,16\] và \[ - 6, - 16\].
Vậy tất cả cặp \[\left( {b,c} \right)\] thỏa mãn là \[\left( {b,c} \right) \in \left\{ {\left( { - 10,16} \right);\left( { - 6, - 16} \right)} \right\}\].
Lời giải
Ta có nhận xét sau
\[{\left( {\frac{1}{{\sqrt {a + 1} }} + \frac{1}{{\sqrt {b + 1} }}} \right)^2} = \frac{1}{{a + 1}} + \frac{1}{{b + 1}} + \frac{2}{{\sqrt {\left( {1 + a} \right)\left( {1 + b} \right)} }}\]
\[ = \frac{{a + b + 2}}{{ab + a + b + 1}} + \frac{2}{{\sqrt {ab + a + b + 1} }} \le \frac{{a + b + 2}}{{a + b + 1}} + \frac{2}{{\sqrt {a + b + 1} }}\]\[ = {\left( {1 + \frac{1}{{\sqrt {a + b + 1} }}} \right)^2}\]
Do đó ta được \[\frac{1}{{\sqrt {a + 1} }} + \frac{1}{{\sqrt {b + 1} }} \le 1 + \frac{1}{{\sqrt {a + b + 1} }}\].
Mặt khác, ta có \[{\left( {a + b + c} \right)^2} \ge {a^2} + {b^2} + {c^2} = 1\] suy ra \[a + b \ge 1 - c\].
Từ đây kết hợp với \[c \le 1\] (vì \[c \ge 0\] và \[{c^2} \le 1\]), ta suy ra
\[P \le 1 + \frac{1}{{\sqrt {2 - c} }} + \frac{1}{{\sqrt {c + 2} }}\]\[ = 1 + \sqrt {{{\left( {\frac{1}{{\sqrt {2 - c} }} + \frac{1}{{\sqrt {c + 2} }}} \right)}^2}} \]\[ = 1 + \sqrt {\frac{1}{{2 - c}} + \frac{1}{{2 + c}} + \frac{2}{{\sqrt {4 - {c^2}} }}} \]
\[ = 1 + \sqrt {\frac{4}{{4 - {c^2}}} + \frac{2}{{\sqrt {4 - {c^2}} }}} \]\[ \le 1 + \sqrt {\frac{4}{{4 - 1}} + \frac{2}{{\sqrt {4 - 1} }}} \]\[ = 2 + \frac{1}{{\sqrt 3 }}\]
Dấu bằng xảy ra chẳng hạn khi \[a = b = 0,c = 1\]. Vậy giá trị lớn nhất của \[P\] là \[2 + \frac{1}{{\sqrt 3 }}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.