Đề thi tuyển sinh vào lớp 10 môn Toán năm 2023-2024 Chuyên Vinh - Nghệ An có đáp án
52 người thi tuần này 4.6 107 lượt thi 5 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử vào lớp 10 Toán (chung) Sở GD&ĐT Lạng Sơn lần 1 năm 2026-2027 có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chuyên) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chung) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề thi thử vào lớp 10 trường THCS Văn Quán (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Phú Diễn (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Lê Lợi (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 trường THCS Thịnh Quang (Hà Nội) năm 2025-2026 Tháng 9 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Nông năm học 2025-2026 có đáp án
Danh sách câu hỏi:
Lời giải
a) Điều kiện xác định: \[x \ge 0\]. Đặt \[t = \left( {x - 1} \right)\sqrt x \] phương trình trở thành
\[{x^3} - 2{x^2} + x - 5\left( {x - 1} \right)\sqrt x - 6 = 0\]\[ \Leftrightarrow x{\left( {x - 1} \right)^2} - 5\left( {x - 1} \right)\sqrt x - 6 = 0\]
\[ \Leftrightarrow {t^2} - 5t - 6 = 0\]\[ \Leftrightarrow \left( {t + 1} \right)\left( {t - 6} \right) = 0\]
Trường hợp 1. \[t = - 1\]suy ra \[0 \le x < 1\]. Đặt \[\sqrt x = a\,\,\,\,\,\left( {0 \le a < 1} \right)\], khi đó ta có
\[\left( {x - 1} \right)\sqrt x = - 1\]\[ \Leftrightarrow {a^3} - a + 1 = 0\] (vô lý \[{a^3} + 1 - a > 0\]).
Trường hợp 2. \[t = 6\]. Đặt \[\sqrt x = a\,\,\,\left( {a \ge 0} \right)\], khi đó ta có
\[\left( {x - 1} \right)\sqrt x = 6\]\[ \Leftrightarrow {a^3} - a - 6 = 0\]
\[ \Leftrightarrow \left( {a - 2} \right)\left( {{a^2} + 2a + 3} \right) = 0\]
\[ \Leftrightarrow a = 2\] (vì \[{a^2} + 2a + 3 = {\left( {a + 1} \right)^2} + 2 > 2 > 0\])
\[ \Leftrightarrow x = 4\] (thỏa mãn điều kiện).
Vậy tất cả các nghiệm thỏa mãn phương trình là \[x = 4\].
b) Ta đặt phương trình như sau \(\left\{ \begin{array}{l}5x + y = {x^2}{y^2} - 15\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)\\2x + 3y = 3{x^2}{y^2} - 13xy - 6\,\,\,\,\,(2).\end{array} \right.\)
Trường hợp 1. Nếu \[x = 0\] thì \[ - 15 = y = - 2\] vô lý nên trường hợp này vô nghiệm.
Trường hợp 2. Nếu \[x \ne 0\], ta có biến đổi như sau
\[\left( 1 \right).3 - \left( 2 \right) \Leftrightarrow 13x = 13xy - 39\]\[ \Leftrightarrow xy = x + 3\]\[ \Leftrightarrow y = 1 + \frac{3}{x}\]
Thế \[y = 1 + \frac{3}{x}\] vào phương trình \[\left( 1 \right)\], ta có
\[5x + 1 + \frac{3}{x} = {\left( {x + 3} \right)^2} - 15\]\[ \Leftrightarrow 5{x^2} + x + 3 = x\left( {{x^2} + 6x + 9} \right) - 15x\]
\[ \Leftrightarrow {x^3} + {x^2} - 7x - 3 = 0\]
\[ \Leftrightarrow \left( {x + 3} \right)\left( {{x^2} - 2x - 1} \right) = 0\]
\[ \Leftrightarrow x \in \left\{ { - 3;1 + \sqrt 2 ;1 - \sqrt 2 } \right\}\].
Nếu \[x = - 3\] thì \[y = 1 + \frac{3}{x} = 0\].
Nếu \[x = 1 + \sqrt 2 \] thì \[y = 1 + \frac{3}{x} = - 2 + 3\sqrt 2 .\]
Nếu \[x = 1 - \sqrt 2 \] thì \[y = 1 + \frac{3}{x} = - 2 - 3\sqrt 2 .\]
Vậy tất cả các nghiệm \[\left( {x;y} \right)\]thỏa mãn là \[\left( { - 3;0} \right);\left( {1 + \sqrt 2 , - 2 + 3\sqrt 2 } \right);\left( {1 - \sqrt 2 , - 2 - 3\sqrt 2 } \right).\]
Lời giải
a) Ta biến đổi phương trình như sau
\({x^2} - {y^2} + 2\left( {3x + y} \right) = 23\)\( \Leftrightarrow \left( {{x^2} + 6x + 9} \right) - \left( {{y^2} - 2y + 1} \right) = 31\)\( \Leftrightarrow {\left( {x + 3} \right)^2} - {\left( {y - 1} \right)^2} = 31\)\( \Leftrightarrow \left( {x - y + 4} \right)\left( {x + y + 2} \right) = 31\)
Từ đây, ta xét bảng sau \[\]
|
\[x - y + 4\] |
31 |
1 |
\[ - 31\] |
\[ - 1\] |
|
\[x + y + 2\] |
1 |
31 |
\[ - 1\] |
\[ - 31\] |
|
\[x\] |
13 |
13 |
\[ - 19\] |
\[ - 19\] |
|
\[y\] |
\[ - 14\] |
16 |
16 |
\[ - 14\] |
Vậy tất cả các nghiệm \[\left( {x,y} \right)\]thỏa mãn là \[\left( {13, - 14} \right);\left( {13,16} \right);\left( { - 19,16} \right);\left( { - 19, - 14} \right)\].
b) Gọi hai nghiệm nguyên của \(P\left( x \right) = {x^2} + bx + c\) là \[u,v\].
Theo định lý Vi – et ta được \[u + v = - b\], \[uv = c\].
Vì \[\left| {P\left( 9 \right)} \right|\] là số nguyên tố nên \[\left| {\left( {9 - u} \right)\left( {9 - v} \right)} \right|\] là số nguyên tố dẫn đến \[\left| {9 - u} \right| = 1\] hoặc \[\left| {9 - v} \right| = 1\].
Không mất tính tổng quát, ta giả sử \[\left| {9 - u} \right| = 1 \Leftrightarrow u \in \left\{ {8;10} \right\}\].
Trường hợp 1. \[u = 10\], vì \[\left| c \right| \le 16\], nên \[\left| v \right| \in \left\{ {0;1} \right\}\]\[ \Leftrightarrow v \in \left\{ { - 1;0;1} \right\}\].
Mặt khác \[9 - 1 = 8,\]\[9 - 0 = 9,\]\[9 + 1 = 10\] đều không là số nguyên tố nên trường hợp này loại.
Trường hợp 2. \[u = 8\], vì \[\left| c \right| \le 16\], nên \[\left| v \right| \le 2\].
Mà \[v\] phải là số chẵn nên từ đây suy ra \[v \in \left\{ { - 2;2} \right\}\]. Thử lại cả hai giá trị này thỏa mãn và ta nhận được giá trị của \[b,c\] tương ứng là \[ - 10,16\] và \[ - 6, - 16\].
Vậy tất cả cặp \[\left( {b,c} \right)\] thỏa mãn là \[\left( {b,c} \right) \in \left\{ {\left( { - 10,16} \right);\left( { - 6, - 16} \right)} \right\}\].
Lời giải
Ta có nhận xét sau
\[{\left( {\frac{1}{{\sqrt {a + 1} }} + \frac{1}{{\sqrt {b + 1} }}} \right)^2} = \frac{1}{{a + 1}} + \frac{1}{{b + 1}} + \frac{2}{{\sqrt {\left( {1 + a} \right)\left( {1 + b} \right)} }}\]
\[ = \frac{{a + b + 2}}{{ab + a + b + 1}} + \frac{2}{{\sqrt {ab + a + b + 1} }} \le \frac{{a + b + 2}}{{a + b + 1}} + \frac{2}{{\sqrt {a + b + 1} }}\]\[ = {\left( {1 + \frac{1}{{\sqrt {a + b + 1} }}} \right)^2}\]
Do đó ta được \[\frac{1}{{\sqrt {a + 1} }} + \frac{1}{{\sqrt {b + 1} }} \le 1 + \frac{1}{{\sqrt {a + b + 1} }}\].
Mặt khác, ta có \[{\left( {a + b + c} \right)^2} \ge {a^2} + {b^2} + {c^2} = 1\] suy ra \[a + b \ge 1 - c\].
Từ đây kết hợp với \[c \le 1\] (vì \[c \ge 0\] và \[{c^2} \le 1\]), ta suy ra
\[P \le 1 + \frac{1}{{\sqrt {2 - c} }} + \frac{1}{{\sqrt {c + 2} }}\]\[ = 1 + \sqrt {{{\left( {\frac{1}{{\sqrt {2 - c} }} + \frac{1}{{\sqrt {c + 2} }}} \right)}^2}} \]\[ = 1 + \sqrt {\frac{1}{{2 - c}} + \frac{1}{{2 + c}} + \frac{2}{{\sqrt {4 - {c^2}} }}} \]
\[ = 1 + \sqrt {\frac{4}{{4 - {c^2}}} + \frac{2}{{\sqrt {4 - {c^2}} }}} \]\[ \le 1 + \sqrt {\frac{4}{{4 - 1}} + \frac{2}{{\sqrt {4 - 1} }}} \]\[ = 2 + \frac{1}{{\sqrt 3 }}\]
Dấu bằng xảy ra chẳng hạn khi \[a = b = 0,c = 1\]. Vậy giá trị lớn nhất của \[P\] là \[2 + \frac{1}{{\sqrt 3 }}\].
Lời giải
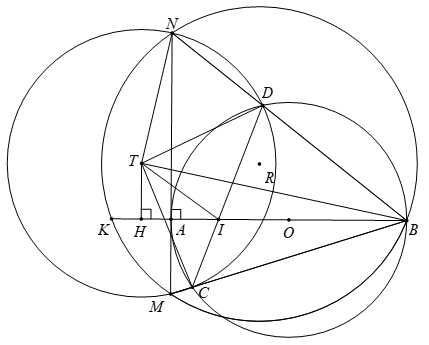
a) Áp dụng hệ thức lượng cho hai tam giác \[BAM\] và \[BAN\] với hai đường cao tương ứng là \[AC,AD\] ta có \[B{A^2} = BC.BM = BD.BN\]. Vì vậy tứ giác \[CDNM\] nội tiếp.
b) Ta có biến đổi góc \[\widehat {MKB} = \widehat {MNB} = \widehat {DCB}\], vì vậy tứ giác \[CIKM\] nội tiếp.
Do đó \[BC.BM = BI.BK = B{A^2}\], từ đây suy ra \[K\] là điểm cố định.
Từ đây ta suy ra \[AM.AN = AK.AB\] cố định.
c) Gọi \[r\] là bán kính của \[\left( T \right)\] thì \[{r^2} - T{A^2} = AN.AM = a\] không đổi. Ta cũng có \[ID.IC\] không đổi, đặt \[b = ID.IC = {r^2} - T{I^2}\] suy ra \[T{I^2} - T{A^2} = a - b\].
Gọi \[H\] là hình chiếu của \[K\]lên \[AB\] theo định lý Pythagore ta có.
\[\left( {AI + 2AH} \right).AI = H{I^2} - H{A^2}\]\[ = \left( {T{I^2} - T{H^2}} \right) - \left( {T{A^2} - T{H^2}} \right)\]\[ = T{I^2} - T{A^2} = a - b\]
Từ đây kết hợp với \[AI\] không đổi (\[A\] và \[I\] cố định) suy ra \[H\] cố định do đó \[BH\]không đổi.
Khi đó, theo định lý Pytagore ta có.
\[B{T^2} = T{H^2} + B{H^2} \ge B{H^2}.\]
Dấu bằng xảy ra khi và chỉ khi \[T\] trùng với \[H\] tức là \[BA\]là trung trực của \[CD\] suy ra \[CD\] vuông góc \[AB\] tại \[I\]. Vậy khi \[CD\] vuông góc với \[AB\] tại \[I\] thì độ dài đoạn thẳng \[BT\] nhỏ nhất.
Lời giải
Trước hết, ta đếm số phần tử thuộc M mà chia hết cho 3.
Ứng với các số có chữ số hàng chục là 1, 4, 7 có 9 số thỏa mãn.
Ứng với các số có chữ số hàng chục là 2, 5, 8 có 9 số thỏa mãn.
Ứng với các số có chữ số hàng chục là 3, 6, 9 có 9 số thỏa mãn.
Vì vậy số phần tử chia hết cho 3 thuộc M là 27 , ta chứng minh |A|max = 30, thật vậy. Trước hết, A không thể chứa quá 4 phần tử không chia hết cho 3 bởi vì tích của chúng sẽ không chia hết cho 3. Do đó, |A| 6 30.
Xây dựng dấu bằng. Xét A là tập hợp các số có 2 chữ số khác nhau chia hết cho 3 và 3 phần tử bất kỳ thuộc các số còn lại.