(0,5 điểm) Một tấm bìa cứng hình chữ nhật có chiều dài là \({\rm{50 cm}}\)và chiều rộng là \({\rm{30 cm}}\). Bạn Linh cắt ở mỗi góc một tấm bìa hình vuông cạnh \(x{\rm{ }}\left( {{\rm{cm}}} \right)\) và xếp phần còn lại thành một hình hộp không nắp. Tìm \(x\) để diện tích xung quanh của hình hộp chữ nhật sau khi cắt là lớn nhất.
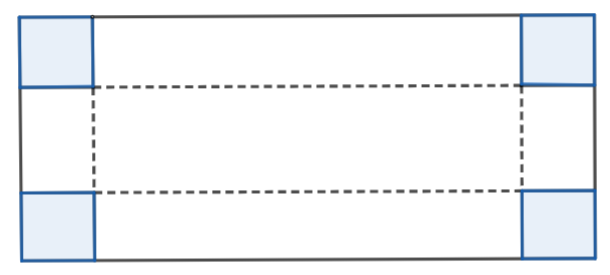
(0,5 điểm) Một tấm bìa cứng hình chữ nhật có chiều dài là \({\rm{50 cm}}\)và chiều rộng là \({\rm{30 cm}}\). Bạn Linh cắt ở mỗi góc một tấm bìa hình vuông cạnh \(x{\rm{ }}\left( {{\rm{cm}}} \right)\) và xếp phần còn lại thành một hình hộp không nắp. Tìm \(x\) để diện tích xung quanh của hình hộp chữ nhật sau khi cắt là lớn nhất.
Câu hỏi trong đề: Bộ 5 đề thi cuối kì 1 Toán 9 Cánh diều (Tự luận) có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Diện tích tấm bìa hình chữ nhật này là: \(50.30 = 1500{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^2}} \right)\)
Chiều dài sau khi cắt tấm bìa là: \(50 - 2x{\rm{ }}\left( {{\rm{cm}}} \right)\).
Chiều rộng sau khi cắt tấm bìa là: \(30 - 2x{\rm{ }}\left( {{\rm{cm}}} \right)\).
Diện tích xung quanh của hộp là: \(2x\left( {50 - 2x + 30 - 2x} \right) = 2x\left( {80 - 4x} \right) = - 8{x^2} + 160x{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^2}} \right)\).
Để diện tích xung quanh của hình hộp chữ nhật sau khi cắt là lớn nhất thì \( - 8{x^2} + 160x\) đạt giá trị lớn nhất.
Ta có: \( - 8{x^2} + 160x = - 8\left( {{x^2} - 20x + 100} \right) + 800 = - 8{\left( {x - 10} \right)^2} + 800\)
Với mọi \(x > 0,\) ta có: \( - 8{\left( {x - 10} \right)^2} \le 0\) nên \( - 8{\left( {x - 10} \right)^2} + 800 \le 800\).
Dấu “=” xảy ra khi \(x - 10 = 0\) hay \(x = 10\).
Vậy diện tích xung quanh hình hộp chữ nhật là \(800{\rm{ c}}{{\rm{m}}^2}\) khi \(x = 10{\rm{ cm}}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Điều kiện xác định \(x \ne - 1,\,\,x \ne 1.\)
Ta có: \(\frac{{x - 1}}{{x + 1}} - \frac{{x + 1}}{{x - 1}} = \frac{4}{{1 - {x^2}}}\)
\[\frac{{{{\left( {x - 1} \right)}^2}}}{{\left( {x + 1} \right)\left( {x - 1} \right)}} - \frac{{{{\left( {x + 1} \right)}^2}}}{{\left( {x + 1} \right)\left( {x - 1} \right)}} = \frac{{ - 4}}{{\left( {x + 1} \right)\left( {x - 1} \right)}}\]
\(\frac{{{{\left( {x - 1} \right)}^2} - {{\left( {x + 1} \right)}^2}}}{{\left( {x + 1} \right)\left( {x - 1} \right)}} = \frac{{ - 4}}{{\left( {x + 1} \right)\left( {x - 1} \right)}}\)
\({\left( {x - 1} \right)^2} - {\left( {x + 1} \right)^2} = - 4\)
\(\left( {x - 1 + x + 1} \right)\left( {x - 1 - x - 1} \right) = - 4\)
\(2x.\left( { - 2} \right) = - 4\)
\( - 4x = - 4\)
\(x = 1\) (không thỏa mãn).
Vậy phương trình đã cho vô nghiệm.Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
![a) Chứng minh bốn điểm \[A,M,O,N\] cùng thuộc một đường tròn. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/12/2-1766542632.png)
a) Vì \(AM,\,\,AN\) là hai tiếp tuyến của đường tròn \(\left( O \right)\) lần lượt tại \(M,\,\,N\) nên \(AM \bot OM,\,\,AN \bot ON.\)
Gọi \[E\] là trung điểm của \[OA\]. Khi đó \(OE = AE = \frac{1}{2}OA.\)
Xét \[\Delta MOA\] vuông tại \[M\] có \[ME\] là đường trung tuyến ứng với cạnh huyền \(OA\) nên \[ME = \frac{1}{2}OA\].
Xét \[\Delta NOA\] vuông tại \[N\] có \[NE\] là đường trung tuyến ứng với cạnh huyền \(OA\) nên \[NE = \frac{1}{2}OA\].
Vì \[NE = ME = OE = AE = \frac{1}{2}OA\] nên bốn điểm \[A,M,O,N\] cùng thuộc đường tròn tâm \[E,\] đường kính \[OA\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập