Cho tam giác ABC vuông tại A với AB = c, AC = b. Vẽ đường tròn tâm O1 đường kính AB và đường tròn tâm O2 đường kính AC. Gọi H là giao điểm thứ hai của hai đường tròn (O1) và (O2). Đường thẳng d thay đổi luôn đi qua A cắt các đường tròn (O1) và (O2) lần lượt tại các điểm D, E không trùng với A sao cho A nằm giữa D,E.
a) Chứng minh rằng đường trung trực của đoạn thẳng DE luôn đi qua một điểm cố định khi đường thẳng (d) thay đổi.
b) Xác định vị trí của đường thẳng (d) để diện tích tứ giác BDEC đạt giá trị lớn nhất. Tìm giá trị lớn nhất đó theo b,c.
c) Kẻ đường thẳng đi qua trung điểm của đoạn DE và vuông góc với BC tại K. Chứng minh rằng
Quảng cáo
Trả lời:
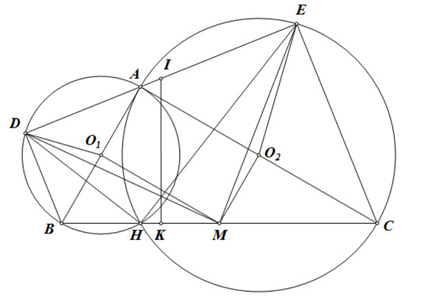
a) Gọi M là trung điểm \(BC \Rightarrow M{O_1} = \frac{1}{2}AC;M{O_2} = \frac{1}{2}AB.\)
Do D thuộc đường tròn đường kính AB nên tam giác ADB vuông tại D.
\( \Rightarrow D{O_1} = \frac{1}{2}AB = M{O_2}.\)Tương tự thì \(E{O_2} = M{O_1}\)
Có tam giác ABC vuông tại A (giả thiết). \(\widehat {ADB} + \widehat {EAC} = {90^o}\)
Mà tam giác DAB vuông tại D nên \(\widehat {ADB} + \widehat {DBA} = {90^o}\) \(\widehat {EAC} = \widehat {ABD} \Rightarrow 2\widehat {EAC} = 2\widehat {ABD} \Rightarrow \widehat {D{O_1}A} = \widehat {E{O_2}C} \Rightarrow \widehat {D{O_1}B} = \widehat {E{O_2}A}\)
Dễ thấy \(M{O_1}//AC,M{O_2}//AB \Rightarrow \widehat {M{O_1}B} = \widehat {M{O_2}A} = {90^o} \Rightarrow \widehat {M{O_1}D} = \widehat {M{O_2}E}\)
Xét \(\Delta M{O_1}D\) và \(\Delta E{O_2}M\) có:
\(M{O_1} = E{O_2}\) (cmt)
\(\widehat {D{O_1}M} = \widehat {M{O_2}E}\) (cmt)
\(D{O_1} = M{O_2}\) (cmt)
\( \Rightarrow \Delta M{O_1}D = \)\(\Delta E{O_2}M\) (c.g.c)
\( \Rightarrow MD = ME\) (2 cạnh tương ứng).
\( \Rightarrow M\) thuộc trung trực DE. Do đó trung trực DE luôn đi qua M cố định (đpcm).
b) Có \(2{S_{BDEC}} = 2{S_{BDA}} + 2{S_{BAC}} + 2{S_{AEC}} = DB.DA + AB.AC + EA.EC \le \frac{1}{2}\left( {B{D^2} + D{A^2}} \right) + \frac{1}{2}\left( {E{A^2} + E{C^2}} \right) + bc\) \(\begin{array}{l} = \frac{1}{2}\left( {A{B^2} + A{C^2}} \right) + bc = \frac{1}{2}\left( {{b^2} + {c^2}} \right) + bc = \frac{1}{2}{\left( {b + c} \right)^2}\\ \Rightarrow {S_{BDEC}} \le \frac{1}{4}{\left( {b + c} \right)^2} \Rightarrow Max = \frac{1}{4}{\left( {b + c} \right)^2}\end{array}\)
Dấu "=" xảy ra \( \Leftrightarrow DA = DB,EA = EC. \Leftrightarrow \) d tạo với AB một góc 45°.
c) Ta có điều phải chứng minh: \(K{B^2} = B{D^2} + K{H^2} \Leftrightarrow I{B^2} - K{I^2} = I{B^2} - I{D^2} + I{H^2} - I{K^2} \Leftrightarrow I{H^2} = I{D^2} \Rightarrow IH = ID = IE\)
Do đó tam giác DHE vuông tại H.
Thật vậy, có \(\widehat {DHB} + \widehat {EHC} = \widehat {DAB} + \widehat {EAC} = {90^o} \Rightarrow \widehat {DHE} = {90^o}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Áp dụng bất đẳng thức AM - GM:
\(\frac{{2x}}{{\sqrt {1 + {x^2}} }} = \frac{x}{{\sqrt {{x^2} + xy + yz + zx} }} = \frac{{2x}}{{\sqrt {\left( {x + y} \right)\left( {x + z} \right)} }}\) \( \le \) \(\frac{x}{{x + y}} + \frac{x}{{x + z}}\)
\(\frac{y}{{\sqrt {{y^2} + xy + yz + zx} }} = \frac{y}{{\sqrt {\left( {y + x} \right)\left( {y + z} \right)} }}\) \( \le \) \(\frac{1}{4}.\frac{y}{{y + z}} + \frac{x}{{y + x}}\)
\(\frac{z}{{\sqrt {{z^2} + xy + yz + zx} }} = \frac{z}{{\sqrt {\left( {z + x} \right)\left( {z + y} \right)} }}\) \( \le \) \(\frac{1}{4}.\frac{z}{{z + y}} + \frac{x}{{z + x}}\)
\(\frac{{2x}}{{\sqrt {1 + {x^2}} }} + \frac{y}{{\sqrt {{y^2} + 1} }} + \frac{z}{{\sqrt {{z^2} + 1} }}\) \( \le \) 1 + 1 + \(\frac{1}{4}\) = \(\frac{9}{4}\) (1)
Và ta có: \({x^2} + 28{y^2} + 28{z^2} = \frac{1}{2}{\left( {x - 7x} \right)^2} + \frac{1}{2}{\left( {x - 7z} \right)^2} + \frac{7}{2}{\left( {y - z} \right)^2} + 7 \ge 7{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( 2 \right)\)
Dấu "=" của các bất đẳng thức (1), (2) xảy ra khi \(x = 7y = 7z\)và \(xy + yz + zx = 1\) khi và chỉ khi
\(y = z = \frac{{\sqrt {15} }}{{15}}\);\(x = \frac{{7\sqrt {15} }}{{15}}\)
Từ (1), (2) có \(P < \frac{9}{4} - 7 = - \frac{{19}}{4}\) suy ra MaxP = 7 \( \Leftrightarrow y = z = \frac{{\sqrt {15} }}{{15}}\;\); \(x = \frac{{7\sqrt {15} }}{{15}}\)
Lời giải
a) Từ giả thiết ta có
\(\begin{array}{l}\left\{ {\begin{array}{*{20}{c}}{{x^2} + {y^2} = 3xy}\\{{x^3} + {y^3} = 10xy}\end{array}} \right. \Rightarrow \left( {x + y} \right)\left( {{x^2} + {y^2}} \right) = 3xy\left( {x + y} \right) \Rightarrow {x^3} + {y^3} + xy\left( {x + y} \right) = 3xy\left( {x + y} \right)\\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \Leftrightarrow 10xy = 2xy\left( {x + y} \right) \Leftrightarrow x + y = 5\left( {x,y \ne 0} \right)\end{array}\) Ta có \({\left( {x + y} \right)^2} = {x^2} + {y^2} + 2xy = 5xy \Rightarrow xy = 5 \Rightarrow \frac{{x + y}}{{xy}} = \frac{1}{x} + \frac{1}{y} = 1\)(đpcm)
a) Theo định lý Bezout: \(P\left( x \right) - 6 = S\left( x \right)\left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right)\)
Do P bậc 3 \( \Rightarrow S\left( x \right) = a\). và \(P\left( { - 1} \right) = a\left( { - 2} \right)\left( { - 3} \right)\left( { - 4} \right) + 6 = - 18 \Rightarrow a = 1\)
Suy ra \(P\left( x \right) = \left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right) + 6 = {x^3} - 6{x^2} + 11x\)
Thử lại ta thấy đúng.
Vậy \(P\left( x \right) = {x^3} - 6{x^2} + 11x\)
c) Đặt \(\left( {\sqrt a ,\sqrt b ,\sqrt c } \right) = \left( {x,y,z} \right)\)điều kiện: \(x,y,z \ge 0\)
\( \Rightarrow x + y + z = 8;{x^2} + {y^2} + {z^2} = 26;{x^2}{y^2}{z^2} = 144\)
\( \Rightarrow x + y + z = 8;xy + yz + zx = \frac{{{{\left( {x + y + z} \right)}^2} - \left( {{x^2} + {y^2} + {z^2}} \right)}}{2} = 19;xyz = 12\)(Do \(x,y,z \ge 0\))
Ta có:\(P = \frac{1}{{yz - x + 9}} + \frac{1}{{xz - y + 9}} + \frac{1}{{xy - z + 9}}\)
Ta có: \(yz - x + 9 = yz - x + x + y + z + 1 = \left( {z + 1} \right)\left( {y + 1} \right)\)
Tương tự: \(xz - y + 9 = \left( {x + 1} \right)\left( {z + 1} \right);xy - z + 9 = \left( {x + 1} \right)\left( {y + 1} \right)\)
\( \Rightarrow \frac{{x + 1 + y + 1 + z + 1}}{{\left( {x + 1} \right)\left( {y + 1} \right)\left( {z + 1} \right)}} = \)\(\frac{{x + y + z + 3}}{{xyz + x + y + z + xy + yz + xz + 1}}\) = \(\frac{{11}}{{12 + 19 + 8 + 1}}\) = \(\frac{{11}}{{40}}\)
Vậy P = \(\frac{{11}}{{40}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.