Cho 3 số thực dương x,y,z thoả mãn \(xy + yz + zx = 1\). Tìm giá trị lớn nhất của biểu thức:

P = \(\frac{{2x}}{{\sqrt {1 + {x^2}} }} + \frac{y}{{\sqrt {{y^2} + 1} }} + \frac{z}{{\sqrt {{z^2} + 1} }} - {x^2} - 28{y^2} - 28{z^2}\)

 

a) Điều kiện: \(x \ge \frac{6}{5}\)

Từ giả thiết ta có: \( - {x^2} + 5x - 6 = 4x\left( {\sqrt {5x - 6}  - x} \right)\) \( \Leftrightarrow  - {x^2} + 5x - 6 = 4x.\frac{{ - {x^2} + 5x - 6}}{{\sqrt {5x - 6}  + x}}\)

Vì \(x \ge \frac{6}{5}\) nên phương trình tương đương: \( \Leftrightarrow \left( {x - 2} \right)\left( {x - 3} \right)\left( {1 - \frac{{ - {x^2} + 5x - 6}}{{x + \sqrt {5x - 6} }}} \right) = 0\)

 Do đó x = 2 hoặc x = 3 (thoả mãn điều kiện) hoặc: \(3x = \sqrt {5x - 6\;} \)  (*)

Giải phương trình (*): \(9{x^2} = 5x - 6 \Leftrightarrow x\left( {x - \frac{5}{9}} \right) + \frac{2}{3} = 0\) ( vô nghiệm vì x ≥ \(\frac{6}{5}\) > \(\frac{5}{9}\))

Vậy phương trình có nghiệm x = 2 và x = 3

b) \(\left\{ {\begin{array}{*{20}{c}}{{x^3} - x{y^2} - 6y = 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( 1 \right)}\\{\left( {x + y} \right)\left( {x + 2y} \right) = 3\left( {xy + 2} \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( 2 \right)}\end{array}} \right.\)

Xét (2): \(\left( {x + y} \right)\left( {x + 2y} \right) = 3\left( {xy + 2} \right) \Leftrightarrow {x^2} + 2{y^2} = 6\)

Từ (1): \({x^3} - x{y^2} - y\left( {{x^2} + 2{y^2}} \right) = 0 \Leftrightarrow {x^3} - x{y^2} - {\rm{y}}{{\rm{x}}^2} - 2{y^3} = 0\)

\( \Leftrightarrow \left( {x - 2y} \right)\left( {{x^2} + xy + {y^2}} \right) = 0\)

Ta để ý (x, y) = (0,0) không là nghiệm của hệ

do đó \({x^2} + xy + {y^2} = {\left( {x + \frac{y}{2}} \right)^2} + \frac{3}{4}{y^2} > 0\).

 Vậy \(x = 2y \Rightarrow 6{y^2} = 6 \Rightarrow y =  \pm 1\)

Nếu \(y = 1 \Rightarrow x = 2\) (Thử lại thoả mãn )

Nếu \(y =  - 1 \Rightarrow x =  - 2\)(Thử lại thoả mãn)

Vậy (x,y) = (2,1) và (x,y) = (−2,−1) là nghiệm của hệ.

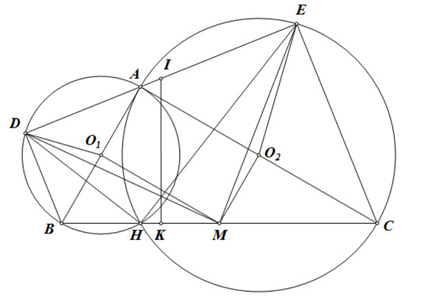
a)     Gọi M là trung điểm \(BC \Rightarrow M{O_1} = \frac{1}{2}AC;M{O_2} = \frac{1}{2}AB.\)

Do D thuộc đường tròn đường kính AB nên tam giác ADB vuông tại D.

\( \Rightarrow D{O_1} = \frac{1}{2}AB = M{O_2}.\)Tương tự thì \(E{O_2} = M{O_1}\)

Có tam giác ABC vuông tại A (giả thiết). \(\widehat {ADB} + \widehat {EAC} = {90^o}\)

Mà tam giác DAB vuông tại D nên \(\widehat {ADB} + \widehat {DBA} = {90^o}\)  \(\widehat {EAC} = \widehat {ABD} \Rightarrow 2\widehat {EAC} = 2\widehat {ABD} \Rightarrow \widehat {D{O_1}A} = \widehat {E{O_2}C} \Rightarrow \widehat {D{O_1}B} = \widehat {E{O_2}A}\)

Dễ thấy \(M{O_1}//AC,M{O_2}//AB \Rightarrow \widehat {M{O_1}B} = \widehat {M{O_2}A} = {90^o} \Rightarrow \widehat {M{O_1}D} = \widehat {M{O_2}E}\)

Xét \(\Delta M{O_1}D\) và \(\Delta E{O_2}M\) có:

\(M{O_1} = E{O_2}\)  (cmt)

\(\widehat {D{O_1}M} = \widehat {M{O_2}E}\) (cmt)

\(D{O_1} = M{O_2}\) (cmt)

\( \Rightarrow \Delta M{O_1}D = \)\(\Delta E{O_2}M\) (c.g.c)

\( \Rightarrow MD = ME\) (2 cạnh tương ứng).

\( \Rightarrow M\) thuộc trung trực DE. Do đó trung trực DE luôn đi qua M cố định (đpcm).

b) Có \(2{S_{BDEC}} = 2{S_{BDA}} + 2{S_{BAC}} + 2{S_{AEC}} = DB.DA + AB.AC + EA.EC \le \frac{1}{2}\left( {B{D^2} + D{A^2}} \right) + \frac{1}{2}\left( {E{A^2} + E{C^2}} \right) + bc\) \(\begin{array}{l} = \frac{1}{2}\left( {A{B^2} + A{C^2}} \right) + bc = \frac{1}{2}\left( {{b^2} + {c^2}} \right) + bc = \frac{1}{2}{\left( {b + c} \right)^2}\\ \Rightarrow {S_{BDEC}} \le \frac{1}{4}{\left( {b + c} \right)^2} \Rightarrow Max = \frac{1}{4}{\left( {b + c} \right)^2}\end{array}\)

Dấu "=" xảy ra \( \Leftrightarrow DA = DB,EA = EC. \Leftrightarrow \) d tạo với AB một góc 45°.

c) Ta có điều phải chứng minh: \(K{B^2} = B{D^2} + K{H^2} \Leftrightarrow I{B^2} - K{I^2} = I{B^2} - I{D^2} + I{H^2} - I{K^2} \Leftrightarrow I{H^2} = I{D^2} \Rightarrow IH = ID = IE\)

Do đó tam giác DHE vuông tại H.

Thật vậy, có \(\widehat {DHB} + \widehat {EHC} = \widehat {DAB} + \widehat {EAC} = {90^o} \Rightarrow \widehat {DHE} = {90^o}\)