Trong không gian \(Oxyz\), cho mặt phẳng \(\left( \alpha \right):x + 2z - 3 = 0\). Điểm nào dưới đây không thuộc mặt phẳng \(\left( \alpha \right)\)?
Quảng cáo
Trả lời:
Đáp án đúng là: D
Thay tọa độ điểm \[M\left( {1;1;0} \right)\] vào phương trình mặt phẳng \(\left( \alpha \right):x + 2z - 3 = 0\) ta được
\(1 + 2.0 - 3 = - 2 \ne 0\). Do đó \(M \notin \left( \alpha \right)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án đúng là: B
Ta có \(V = \pi \int\limits_0^\pi {{{\sin }^2}xdx} = \left. {\pi \left( {\frac{x}{2} - \frac{{\sin 2x}}{4}} \right)} \right|_0^\pi = \pi .\frac{\pi }{2} = \frac{{{\pi ^2}}}{2}\).
Lời giải
Trả lời: 1,3
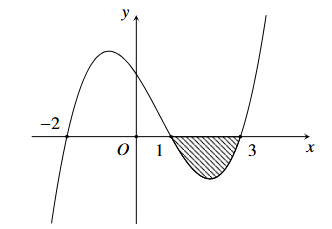
Ta có \(\int\limits_{ - 2}^3 {f'\left( x \right)dx} = \int\limits_{ - 2}^1 {f'\left( x \right)dx} + \int\limits_1^3 {f'\left( x \right)dx} = 3 - \int\limits_1^3 {\left| {f'\left( x \right)} \right|dx} \)\( = 3 - \frac{5}{3} = \frac{4}{3}\).
Mà \(\int\limits_{ - 2}^3 {f'\left( x \right)dx} = \left. {f\left( x \right)} \right|_{ - 2}^3 = f\left( 3 \right) - f\left( { - 2} \right)\).
Do đó \(f\left( 3 \right) - f\left( { - 2} \right) \approx 1,3\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.