Cho hai số nguyên \(p,q\) thỏa mãn đẳng thức \({p^2} + {q^2} = 2\left( {3pq - 4} \right)\) (*)
1) Chứng minh rằng có ít nhất một trong hai số \(p,q\) là bội của 3
2) Tìm tất cả các cặp số nguyên \(\left( {p,q} \right)\) thỏa (*)
Cho hai số nguyên \(p,q\) thỏa mãn đẳng thức \({p^2} + {q^2} = 2\left( {3pq - 4} \right)\) (*)
1) Chứng minh rằng có ít nhất một trong hai số \(p,q\) là bội của 3
2) Tìm tất cả các cặp số nguyên \(\left( {p,q} \right)\) thỏa (*)
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Chứng minh rằng có ít nhất một trong hai số \(p,q\) là bội của 3
· Giả sử trong hai số \(p,q\) không có số nào chia hết cho 3.
· Khi đó \({p^2},\;{q^2}\) chia 3 dư 1. Suy ra:
+) \({p^2} + {q^2}\;\) chia 3 dư 2;
+) Trong khi vế phải \(2\left( {3pq - 4} \right) = 6pq - 9 + 1\) chia 3 dư 1, vô lý
· Do đó tromg hai số \(p,q\) phải có ít nhất một số là bội của 3.
b) Tìm tất cả các cặp số nguyên \(\left( {p,q} \right)\) thỏa (*)
· Do vai trò của \(p,q\) như nhau, không mất tính tổng quát, giả sử \(q\) là bội của 3.
· Do \(q\) nguyên tố nên \(q = 3\)
· Khi đó từ (*) ta có \({p^2} + 9 = 2\left( {2p - 4} \right) \Leftrightarrow {p^2} - 18p + 17 = 0 \Leftrightarrow p = 1\) hoặc \(p = 17\)
· Do \(p\) nguyên tố nên \(p = 17.\)
Vậy các cặp số \(\left( {p;q} \right)\) thỏa mãn (*) là \(\left( {p;q} \right) \in \left\{ {\left( {17;3} \right);\left( {3;17} \right)} \right\}.\)
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
1)Phương trình hoành độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) là
\({x^2} = 2\left( {m - 1} \right)x + 3 \Leftrightarrow {x^2} - 2\left( {m - 1} \right)x - 3 = 0\)
Do \(1.\left( { - 3} \right) = - 3 < 0\) nên phương trình trên luôn có hai nghiệm phân biệt \({x_1},\;{x_2}\)
Do đó đường thẳng \(\left( d \right)\) luôn cắt parabo; \(\left( P \right)\) tại hai điểm phân biệt có hoành độ \({x_1},\;{x_2}.\)
Theo hệ thức Vi-ét, ta có \(\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} = 2\left( {m - 1} \right)\;\;\;\;\;\left( 1 \right)}\\{{x_1}{x_2} = - 3\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( 2 \right)}\end{array}} \right.\)
Lấy \({x_1} + 2{x_2} = 5\) trừ (1) vế theo vế ta được \(\left\{ {\begin{array}{*{20}{c}}{{x_2} = 7 - 2m\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\\{{x_1} = 2\left( {m - 1} \right) - \left( {7 - 2m} \right) = 4m - 9}\end{array}} \right.\)
Thay vào (2) ta được \(\left( {7 - 2m} \right)\left( {4m - 9} \right) = - 3 \Leftrightarrow - 8{m^2} + 46m - 60 = 0\)
\( \Leftrightarrow 4{m^2} - 23m + 30 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m = 2}\\{m = \frac{{15}}{4}}\end{array}} \right.\)
\({\rm{Vay\;}}m \in \left\{ {2;\frac{{15}}{4}} \right\}\)
2)Ta có \(\left( {a{x^2} + 2bx + c} \right)\left( {b{x^2} + 2cx + a} \right)\left( {c{x^2} + 2ax + b} \right) = 0{\rm{\;}} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{a{x^2} + 2bx + c = 0\;\;\;\;\left( 1 \right)}\\{b{x^2} + 2cx + a = 0\;\;\;\;\left( 2 \right)}\\{c{x^2} + 2ax + b = 0\;\;\;\;\left( 3 \right)}\end{array}} \right.\)
· Trường hợp 1: Nếu \(a.b.c = 0\) thì phương trình đã cho luôn có nghiệm
· Trường hợp 2: Nếu \(a.b.c \ne 0\). , ta có
Khi đó
\( = {\left( {a - b} \right)^2} + {\left( {b - c} \right)^2} + {\left( {c - a} \right)^2} \ge 0\).
Suy ra một trong ba số không âm.
Do đó, một trong ba phương trình (1), (2), (3) có nghiệm nên ta có điều phải chứng minh
3)
a) Chứng minh rằng \(\frac{x}{{\sqrt {x - 1} }}\) \( \ge 2\).
Áp dụng bất đẳng thức \(AM - GM\) cho hai số thực dương \(\left( {x - 1} \right)\) và 1 ta được
\(x = \left( {x - 1} \right) + 1 \ge 2\sqrt {\left( {x - 1} \right).1} = 2\sqrt {x - 1} .\)
Vậy \(\frac{x}{{\sqrt {x - 1} }} \ge 2\) với mọi số thực \(x > 1\). Đẳng thức xảy ra khi và chỉ khi \(x - 1 = 1 \Leftrightarrow x = 2.\)
b) Tìm giá trị nhỏ nhất của biểu thức T = \(\frac{{{x^2}}}{{y - 1}} + \frac{{{y^2}}}{{x - 1}}\)
Áp dụng bất đẳng thức AM – GM cho hai số thực dương \(\frac{{{x^2}}}{{y - 1}}\) và \(\frac{{{y^2}}}{{x - 1}}\) ta được
\(T = \;\frac{{{x^2}}}{{y - 1}} + \frac{{{y^2}}}{{x - 1}} \ge 2\sqrt {\frac{{{x^2}}}{{y - 1}}.\frac{{{y^2}}}{{x - 1}}} = 2.\frac{x}{{\sqrt {x - 1} }}.\frac{y}{{\sqrt {y - 1} }} \ge 2.2.2 = 8\)
Vậy \(\min T = 8\) khi \(x = y = 2.\)
Lời giải
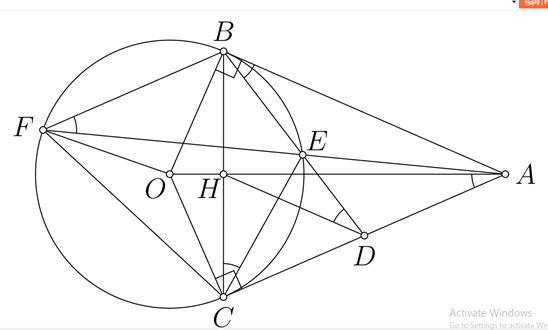
1) Chứng minh CDEH là một tứ giác nội tiếp.
Ta có
· \(AB = AC\) (tính chất hai tiếp tuyến cắt nhau).
· \(OB = OC\;\)(bán kính (O)) nên AO là đường trung trực của đoạn thẳng BC.
· \(\Delta ABC\) có D là trung điểm AC, H là trung điểm BC nên HD là đường trung bình của tam giác ABC, suy ra \(HD//AB\).
Khi đó \(\widehat {HDE} = \widehat {ABE} = \widehat {BCE} = \widehat {HCE} = \frac{1}{2}\;sd\;\widehat {BE}\)
Do đó, tứ giác CDEH nội tiếp.
2) Chứng minh rằng \(D{A^2} = DE.DB\)
Xét \(\Delta DCE\) và \(\Delta DBC\) ta có
\(\widehat {EDC}\;\) chung
\(\widehat {DCE} = \widehat {DBC} = \frac{1}{2}\;sd\;\widehat {BE}\)
Suy ra (g-g)
Do đó \(\frac{{{\rm{DC}}}}{{{\rm{DB}}}} = \frac{{{\rm{DE}}}}{{{\rm{DC}}}}.\) Suy ra \(D{C^2} = DE.DB\)
Mặt khác, do \(DA = DC\) nên \(D{A^2} = DE.DB\)
3) Gọi F là giao điểm thứ hai của AE với đường tròn (O). Chứng minh OC là đường trung trực của đoạn thẳng BF.
· Từ \(D{A^2} = DE.DB\) nên ta có \(\frac{{DA}}{{DE}} = \frac{{DB}}{{DA}}\)
· Xét hai tam giác \(DAE\) và tam giác \(DBA\) có
+) \(\widehat {EDA}\;\) chung;
+) \(\frac{{DA}}{{DE}} = \frac{{DB}}{{DA}}\)
Do đó
· Suy ra \(\widehat {EAD\;} = \widehat {DBA} = \widehat {DFA} = \frac{1}{2}sd\widehat {BE}\), do đó \(BF//AC.\)
· Mà \(OC \bot AC\) nên \(OC \bot BF\).
· Mặt khác, \(OF = OB\) (bán kính của (O)) nên OC là đường trung trực của đoạn thẳng BF.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập