a) Cho a, b là các số thực không âm, c là số thực dương thỏa mãn đẳng thức
\(\sqrt a - \sqrt {a + b - c} = \sqrt b + \sqrt c \)
Chứng minh rằng: \(\sqrt[3]{a} + \sqrt[3]{b} - \sqrt[3]{c} = \sqrt[3]{{a + b - c}}\)
b) Tìm tất cả các số nguyên dương a, b sao cho số \(\frac{{\sqrt 3 + \sqrt a }}{{\sqrt 5 + \sqrt b }}\) là số hữu tỷ.
a) Cho a, b là các số thực không âm, c là số thực dương thỏa mãn đẳng thức
\(\sqrt a - \sqrt {a + b - c} = \sqrt b + \sqrt c \)
Chứng minh rằng: \(\sqrt[3]{a} + \sqrt[3]{b} - \sqrt[3]{c} = \sqrt[3]{{a + b - c}}\)
b) Tìm tất cả các số nguyên dương a, b sao cho số \(\frac{{\sqrt 3 + \sqrt a }}{{\sqrt 5 + \sqrt b }}\) là số hữu tỷ.
Quảng cáo
Trả lời:
a) Bằng các phép biến đổi biểu thức kết hợp với a, b không âm và c thực dương, ta có:
\(\sqrt a - \sqrt {a + b - c} = \sqrt b + \sqrt c \)
\(\;\;\;\;\;\;\; \Leftrightarrow \sqrt a - \sqrt b = \sqrt c + \sqrt {a + b - c} \)
\( \Leftrightarrow a + b - 2\sqrt {ab} = a + b + 2\sqrt {c\left( {a + b - c} \right)} \)
\( \Leftrightarrow \sqrt {ab} + \sqrt {c\left( {a + b - c} \right)} = 0\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{ab = 0}\\{\left( {a + b - c} \right) = 0}\end{array}} \right.\) (*)
Ta cần chứng minh
\(\sqrt[3]{a} + \sqrt[3]{b} - \sqrt[3]{c} = \sqrt[3]{{a + b - c}}\)
Ta biến đổi tương đương đẳng thức này kết hợp với a, b không âm và c thực dương, ta có:
\(\sqrt[3]{a} + \sqrt[3]{b} - \sqrt[3]{c} = \sqrt[3]{{a + b - c}}\)
\( \Leftrightarrow \sqrt[3]{a} + \sqrt[3]{b} = \sqrt[3]{c} + \sqrt[3]{{a + b - c}}\)
\( \Leftrightarrow a + b + 3\left( {\sqrt[3]{{{a^2}b}} + \sqrt[3]{{a{b^2}}}} \right) = a + b + 3\left( {\sqrt[3]{{{c^2}\left( {a + b - c} \right)}} + \sqrt[3]{{c{{(a + b - c)}^2}}}} \right)\)
\( \Leftrightarrow \left( {\sqrt[3]{{{a^2}b}} + \sqrt[3]{{a{b^2}}}} \right) = \left( {\sqrt[3]{{{c^2}\left( {a + b - c} \right)}} + \sqrt[3]{{c{{(a + b - c)}^2}}}} \right)\)
Đẳng thức cuối đúng với điều kiện (*) nên đẳng thức đầu đúng. Bài toán được chứng minh.
b) Lấy sao cho
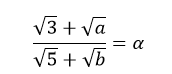
Viết lại phương trình dưới dạng
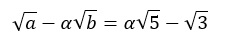
Bình phương 2 vế ta có:
\(a + {\alpha ^2}b - 2\alpha \sqrt {ab} = 5{\alpha ^2} - 2\alpha \sqrt {15} \)
Từ đó suy ra
\(\sqrt {ab} - \sqrt {15} = \beta \in \mathbb{Q}\)
Bình phương 2 vế đẳng thức \(\sqrt {ab} - \sqrt {15} + \beta \) ta được
\(ab = 15 + {\beta ^2} + 2\beta \sqrt {15} \)
\( \Leftrightarrow 2\beta \sqrt {15} = ab - 15 - {\beta ^2}\)
Đẳng thức cuối xảy ra khi và chỉ khi \(\beta \) = 0 tức là ab = 15 . Xét tất cả khả năng có thể xảy ra, ta được.
· a = 1 , b = 15 tức là \(\alpha = \frac{{\sqrt 3 + 1}}{{\sqrt 5 + \sqrt {15} }} = \frac{1}{{\sqrt {5\;} }}\;\)là1 số vô tỷ.
· a = 3, b = 5 tức là \(\alpha = \frac{{2\sqrt 3 }}{{2\sqrt 5 }} = \frac{{\sqrt 3 }}{{\sqrt {5\;} }}\;\;\)là 1 số vô tỷ.
· a = 5, b = 3 tức là \(\alpha = \frac{{\sqrt 3 + \sqrt 5 }}{{\sqrt 5 + \sqrt 3 }} = 1\) là 1 số hữu tỷ.
· a = 15 , b = 1 , tức là \(\alpha = \frac{{\sqrt 3 + \sqrt {15} }}{{\sqrt 5 + 1}} = \sqrt 3 \), 1 số vô tỷ.
Vậy tất cả các cặp (a,b) thỏa mãn là a = 5 b = 3 .
Các bạn có thể tham khảo bài toán gốc của câu 26) như sau. Tìm tất cả các số nguyên dương a, b sao cho số
\(\frac{{\sqrt 2 + \sqrt a }}{{\sqrt 3 + \sqrt b }}\)
là số hữu tỷ.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
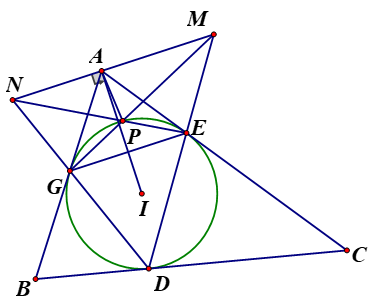
a) Vì AM là phân giác ngoài \(\widehat {BAC}\) . AI là phân giác trong góc A nên AI \( \bot \) AM mà GE // AI nên EG // AM hay GE // MN . Bài toán được chứng minh.
b) Gọi \({P_1}\) là giao của NE và đường tròn (I) thì từ EG // MN, ta có:
\(\widehat {AN{P_1}} = \widehat {ANE} = \widehat {{P_1}EG} = \widehat {{P_1}GA}\)
Do đó tứ giác ANGP, nội tiếp kết hợp với tứ giác DG\({P_1}E\) nội tiếp, ta có
\(\widehat {{P_1}EM} = \widehat {{P_1}GD} = \widehat {NA{P_1}} = 180^\circ - \widehat {{P_1}GA}\)
Suy ra tứ giác MA\({P_1}E\) nội tiếp kết hợp với EG // MN và tứ giác ANG\({P_1}\) nội tiếp, ta có:
\(\widehat {G{P_1}M} = \widehat {A{P_1}M} + \widehat {A{P_1}G} = \widehat {AEM} + \widehat {A{P_1}G} = \widehat {DGE} + \widehat {A{P_1}G} = \widehat {GNA} + \widehat {A{P_1}G} = \;180^\circ \)
Do đó ta được 3 điểm G, \({P_1},\) M thẳng hàng. Vì vậy nên \({P_1}\) trùng P. Nói cách khác MG, NE cắt nhau tại 1 điểm P nằm trên (I). Bài toán được chứng minh.
Lời giải
1) Gọi 4 số nguyên liên tiếp bất kỳ là a, a + 1 , a + 2 a + 3 với a in mathbb Z Ta có các biến đổi:
\(a\left( {a + 1} \right)\left( {a + 2} \right)\left( {a + 3} \right) + 1 = \left( {{a^2} + 3a} \right)\left( {{a^2} + 3a + 2} \right) + 1\)
\( = {({a^2} + 3a)^2} + 2\left( {{a^2} + 3a} \right) + 1\)
\( = {({a^2} + 3a + 1)^2}\)
Vì\(\;\;\;{({a^2} + 3a + 1)^2}\) là một số chính phương nên bài toán được chứng minh.
2) Bằng các phép biến đổi ta được hệ phương trình sau
\(\left\{ {\begin{array}{*{20}{c}}{2xy - x = 10}\\{x + y + xy = 12}\end{array} \Leftrightarrow } \right.\) \(\left\{ {\begin{array}{*{20}{c}}{x\left( {2y - 1} \right) = 10}\\{\left( {x + 1} \right)\left( {y + 1} \right) = 12}\end{array}\;\;\;\;\;\left( 1 \right)} \right.\)
Vì 2, y nguyên nên x , 2y - 1 nguyên do đó 2y - 1 là ước lẻ của 10. Ta xét các trường hợp sau.
· 2y - 1 = 1 suy ra y = 1 và x = 10 thay vào (1) không thỏa mãn.
· 2y - 1 = - 1 suy ra y = 0 và x = - 10 thay vào (1) ta thấy không thỏa mãn.
· 2y - 1 = 5 suy ra y = 3 và x = 2 thay vào (1) ta thấy thỏa mãn.
· 2y - 1 = - 5 suy ra y = - 2 và x = - 2 thay vào (1) ta thấy không thỏa mãn.
Vậy cặp số nguyên (x,y) thỏa mãn duy nhất là (x, y) = (2, 3) .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.