Bảy lục giác đều được sắp xếp và tô màu bằng hai màu trắng, đen như ở Hình 1. Mỗi lần cho phép chọn ra một lục giác đều, đổi màu của lục giác đó và của tất cả các lục giác đều chung cạnh với lục giác đó (trắng thành đen và đen thành trắng). Chứng minh rằng dù có thực hiện cách làm trên bao nhiêu lần đi nữa, cũng không thể nhận được các lục giác đều được ô màu như ở Hình 2.
Bảy lục giác đều được sắp xếp và tô màu bằng hai màu trắng, đen như ở Hình 1. Mỗi lần cho phép chọn ra một lục giác đều, đổi màu của lục giác đó và của tất cả các lục giác đều chung cạnh với lục giác đó (trắng thành đen và đen thành trắng). Chứng minh rằng dù có thực hiện cách làm trên bao nhiêu lần đi nữa, cũng không thể nhận được các lục giác đều được ô màu như ở Hình 2.
Quảng cáo
Trả lời:
Cách 1. Đánh số vào các hình lục giác như hình vẽ.

Ta xét một hình lục giác được điền số \({a_i}\;\;\)thì \({a_i} \equiv {b_i}\) (mod 2) trong đó \({b_i}\) là tổng các số được điền trong các hình lục giác chung cạnh với hình lục giác đang xét. Do đó, khi đổi màu theo đề bài thì số dư trong phép chia cho 2 của tổng các số trong các hình lục giác tô đen luôn không đổi.
Đối với hình 1 thì số dư này bằng 1, còn đối với hình 2 thì số dư này bằng 0 nên không thể có cách đổi màu nào biến hình 1 thành hình 2.
Cách 2.
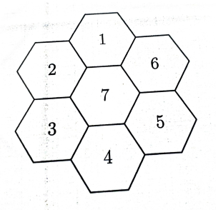
Xét các ô 2,3,5,6. Mỗi bước ta đổi màu hai hoặc cả bốn ô đó nên số ô đen không thay đổi tính chẵn, lẻ. Ban đầu trong bốn ô nói trên có hai ô đen nên không thể có trạng thái trong bốn ô đó có đúng một ô đen.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
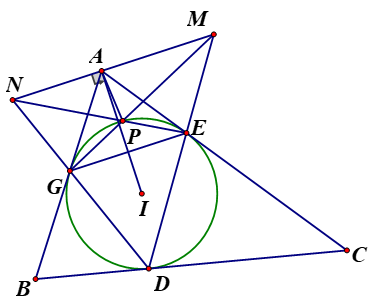
a) Vì AM là phân giác ngoài \(\widehat {BAC}\) . AI là phân giác trong góc A nên AI \( \bot \) AM mà GE // AI nên EG // AM hay GE // MN . Bài toán được chứng minh.
b) Gọi \({P_1}\) là giao của NE và đường tròn (I) thì từ EG // MN, ta có:
\(\widehat {AN{P_1}} = \widehat {ANE} = \widehat {{P_1}EG} = \widehat {{P_1}GA}\)
Do đó tứ giác ANGP, nội tiếp kết hợp với tứ giác DG\({P_1}E\) nội tiếp, ta có
\(\widehat {{P_1}EM} = \widehat {{P_1}GD} = \widehat {NA{P_1}} = 180^\circ - \widehat {{P_1}GA}\)
Suy ra tứ giác MA\({P_1}E\) nội tiếp kết hợp với EG // MN và tứ giác ANG\({P_1}\) nội tiếp, ta có:
\(\widehat {G{P_1}M} = \widehat {A{P_1}M} + \widehat {A{P_1}G} = \widehat {AEM} + \widehat {A{P_1}G} = \widehat {DGE} + \widehat {A{P_1}G} = \widehat {GNA} + \widehat {A{P_1}G} = \;180^\circ \)
Do đó ta được 3 điểm G, \({P_1},\) M thẳng hàng. Vì vậy nên \({P_1}\) trùng P. Nói cách khác MG, NE cắt nhau tại 1 điểm P nằm trên (I). Bài toán được chứng minh.
Lời giải
1) Gọi 4 số nguyên liên tiếp bất kỳ là a, a + 1 , a + 2 a + 3 với a in mathbb Z Ta có các biến đổi:
\(a\left( {a + 1} \right)\left( {a + 2} \right)\left( {a + 3} \right) + 1 = \left( {{a^2} + 3a} \right)\left( {{a^2} + 3a + 2} \right) + 1\)
\( = {({a^2} + 3a)^2} + 2\left( {{a^2} + 3a} \right) + 1\)
\( = {({a^2} + 3a + 1)^2}\)
Vì\(\;\;\;{({a^2} + 3a + 1)^2}\) là một số chính phương nên bài toán được chứng minh.
2) Bằng các phép biến đổi ta được hệ phương trình sau
\(\left\{ {\begin{array}{*{20}{c}}{2xy - x = 10}\\{x + y + xy = 12}\end{array} \Leftrightarrow } \right.\) \(\left\{ {\begin{array}{*{20}{c}}{x\left( {2y - 1} \right) = 10}\\{\left( {x + 1} \right)\left( {y + 1} \right) = 12}\end{array}\;\;\;\;\;\left( 1 \right)} \right.\)
Vì 2, y nguyên nên x , 2y - 1 nguyên do đó 2y - 1 là ước lẻ của 10. Ta xét các trường hợp sau.
· 2y - 1 = 1 suy ra y = 1 và x = 10 thay vào (1) không thỏa mãn.
· 2y - 1 = - 1 suy ra y = 0 và x = - 10 thay vào (1) ta thấy không thỏa mãn.
· 2y - 1 = 5 suy ra y = 3 và x = 2 thay vào (1) ta thấy thỏa mãn.
· 2y - 1 = - 5 suy ra y = - 2 và x = - 2 thay vào (1) ta thấy không thỏa mãn.
Vậy cặp số nguyên (x,y) thỏa mãn duy nhất là (x, y) = (2, 3) .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.