Giải phương trình và hệ phương trình sau:

a) \[3{x^2} + 5x - 12 = 0.\]

b) \(\left\{ \begin{array}{l}2x - y = 7\\x + 2y = 6\end{array} \right..\)

a)Gọi \[x,y\] lần lượt là số học sinh trường THCS A và trường THCS A (ĐK: \[x,y \in {\mathbb{N}^*}\] và\[x,y < 322\]).

Theo đề bài ta có hệ phương trình

\[\left\{ \begin{array}{l}x + y = 322\\6x - 5y = 172\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5x + 5y = 1610\\6x - 5y = 172\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}11x = 1782\\6x - 5y = 172\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 162\\y = 160\end{array} \right.\]

Giải hệ phương trình tìm được \[\left\{ \begin{array}{l}x = 162\\y = 160\end{array} \right.\] (thỏa mãn ĐK)

Vậy số quyển sách của trường THCS A quyên góp được là \[162.6 = 972\]quyển.

Số quyển sách của trường THCS B quyên góp được là \[160.5 = 800\]quyển

b)\[{x^2} - (2m + 1)x + {m^2} + 1 = 0\]

Ta có \(\Delta  = {{\rm{[}} - (2m + 1){\rm{]}}^2} - 4.1.({m^2} + 1) = 4m - 3\)

Phương  trình có hai nghiệm phân biệt khi\(\Delta  > 0\)

\( \Leftrightarrow 4m - 3 > 0 \Leftrightarrow m > \frac{3}{4}\)

Theo hệ thức Viet, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m + 1\\{x_1}.\,{x_2} = {m^2} + 1\end{array} \right.\)

Theo đề bài, ta có:  \[{({x_1} + 1)^2} + {({x_2} + 1)^2} = 13.\]

\[ \Leftrightarrow {x_1}^2 + 2{x_1} + 1 + {x_2}^2 + 2{x_2} + 1 = 13.\]

\[ \Leftrightarrow \left( {{x_1}^2 + {x_2}^2} \right) + 2({x_1} + {x_2}) + 2 = 13\]

\[\begin{array}{l} \Leftrightarrow \left( {{x_1}^2 + {x_2}^2} \right) + 2({x_1} + {x_2}) - 11 = 0\\ \Leftrightarrow {({x_1} + {x_2})^2} - 2{x_1}{x_2} + 2({x_1} + {x_2}) - 11 = 0\\ \Leftrightarrow {(2m + 1)^2} - 2({m^2} + 1) + 2(2m + 1) - 11 = 0\\ \Leftrightarrow 2{m^2} + 8m - 10 = 0\end{array}\]

\[ \Leftrightarrow \left[ \begin{array}{l}m = 1\\m =  - 5\end{array} \right.\]\(\begin{array}{l}{\rm{(Nha\"a n)}}\\{\rm{(Loa\"i i)}}\end{array}\)

Vậy \[m = 1\] thỏa mãn đề bài

a) Rút gọn biểu thức \[Q = \frac{{\sqrt 6  - 2\sqrt 8 }}{{\sqrt 6 }} - {\left( {\sqrt 3  - 1} \right)^2}.\]

\[Q = \frac{{\sqrt 6 \left( {1 - 2\sqrt 3 } \right)}}{{\sqrt 6 }} - \left( {\sqrt {{3^2}}  - 2\sqrt 3  + 1} \right)\]

\[Q = 1 - 2\sqrt 3  - (4 - 2\sqrt 3 )\]

\[Q =  - 3\]

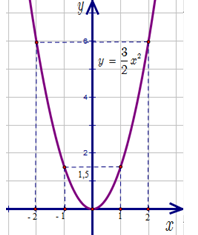
b) Trên mặt phẳng tọa độ \[Oxy\], vẽ đồ thị của hàm số \(y = \frac{3}{2}{x^2}.\)

Bảng giá trị

\(x\).\( - 2\).\( - 1\).\(0\).\(1\).\(2\)

\(y = \frac{3}{2}{x^2}.\).\(6\).\(\frac{3}{2}\).\(0\).\(\frac{3}{2}\).\(6\)