Đề thi tuyển sinh vào lớp 10 môn Toán năm 2023-2024 Cần Thơ có đáp án
76 người thi tuần này 4.6 152 lượt thi 4 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử vào lớp 10 Toán (chung) Sở GD&ĐT Lạng Sơn lần 1 năm 2026-2027 có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chuyên) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chung) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề thi thử vào lớp 10 trường THCS Văn Quán (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Phú Diễn (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Lê Lợi (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 trường THCS Thịnh Quang (Hà Nội) năm 2025-2026 Tháng 9 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Nông năm học 2025-2026 có đáp án
Danh sách câu hỏi:
Lời giải
a) \(3{x^2} + 5x - 12 = 0\)
Ta có \(\Delta = {5^2} - 4.3.( - 12) = 169 > 0\)
Phương trình có hai nghiệm phân biệt
\({x_1} = \frac{{ - 5 + \sqrt {69} }}{{2.3}} = \frac{4}{3};{x_2} = \frac{{ - 5 - \sqrt {69} }}{{2.3}} = - 3\)
Vậy tập nghiệm của phương trình là \(S = \left\{ { - 3;\frac{4}{3}} \right\}\)
b) \(\left\{ \begin{array}{l}2x - y = 7\\x + 2y = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4x - 2y = 14\\x + 2y = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5x = 20\\y = 2x - 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4\\y = 1\end{array} \right.\)
Vậy hệ phương trình có nghiệm duy nhất là \((x;y) = (4;1)\)
Lời giải
a) Rút gọn biểu thức \[Q = \frac{{\sqrt 6 - 2\sqrt 8 }}{{\sqrt 6 }} - {\left( {\sqrt 3 - 1} \right)^2}.\]
\[Q = \frac{{\sqrt 6 \left( {1 - 2\sqrt 3 } \right)}}{{\sqrt 6 }} - \left( {\sqrt {{3^2}} - 2\sqrt 3 + 1} \right)\]
\[Q = 1 - 2\sqrt 3 - (4 - 2\sqrt 3 )\]
\[Q = - 3\]
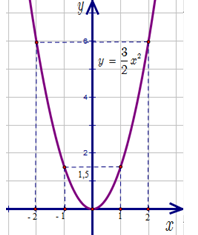
b) Trên mặt phẳng tọa độ \[Oxy\], vẽ đồ thị của hàm số \(y = \frac{3}{2}{x^2}.\)
Bảng giá trị
\(x\).\( - 2\).\( - 1\).\(0\).\(1\).\(2\)
\(y = \frac{3}{2}{x^2}.\).\(6\).\(\frac{3}{2}\).\(0\).\(\frac{3}{2}\).\(6\)
Lời giải
a)Gọi \[x,y\] lần lượt là số học sinh trường THCS A và trường THCS A (ĐK: \[x,y \in {\mathbb{N}^*}\] và\[x,y < 322\]).
Theo đề bài ta có hệ phương trình
\[\left\{ \begin{array}{l}x + y = 322\\6x - 5y = 172\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5x + 5y = 1610\\6x - 5y = 172\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}11x = 1782\\6x - 5y = 172\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 162\\y = 160\end{array} \right.\]
Giải hệ phương trình tìm được \[\left\{ \begin{array}{l}x = 162\\y = 160\end{array} \right.\] (thỏa mãn ĐK)
Vậy số quyển sách của trường THCS A quyên góp được là \[162.6 = 972\]quyển.
Số quyển sách của trường THCS B quyên góp được là \[160.5 = 800\]quyển
b)\[{x^2} - (2m + 1)x + {m^2} + 1 = 0\]
Ta có \(\Delta = {{\rm{[}} - (2m + 1){\rm{]}}^2} - 4.1.({m^2} + 1) = 4m - 3\)
Phương trình có hai nghiệm phân biệt khi\(\Delta > 0\)
\( \Leftrightarrow 4m - 3 > 0 \Leftrightarrow m > \frac{3}{4}\)
Theo hệ thức Viet, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m + 1\\{x_1}.\,{x_2} = {m^2} + 1\end{array} \right.\)
Theo đề bài, ta có: \[{({x_1} + 1)^2} + {({x_2} + 1)^2} = 13.\]
\[ \Leftrightarrow {x_1}^2 + 2{x_1} + 1 + {x_2}^2 + 2{x_2} + 1 = 13.\]
\[ \Leftrightarrow \left( {{x_1}^2 + {x_2}^2} \right) + 2({x_1} + {x_2}) + 2 = 13\]
\[\begin{array}{l} \Leftrightarrow \left( {{x_1}^2 + {x_2}^2} \right) + 2({x_1} + {x_2}) - 11 = 0\\ \Leftrightarrow {({x_1} + {x_2})^2} - 2{x_1}{x_2} + 2({x_1} + {x_2}) - 11 = 0\\ \Leftrightarrow {(2m + 1)^2} - 2({m^2} + 1) + 2(2m + 1) - 11 = 0\\ \Leftrightarrow 2{m^2} + 8m - 10 = 0\end{array}\]
\[ \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = - 5\end{array} \right.\]\(\begin{array}{l}{\rm{(Nha\"a n)}}\\{\rm{(Loa\"i i)}}\end{array}\)
Vậy \[m = 1\] thỏa mãn đề bài
Lời giải
![Cho tam giác \[ABC{\rm{ }}(AB < AC)\]có ba góc nhọn, nội tiếp đường tròn tâm (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/12/blobid2-1766802977.png)
a) Chứng minh tứ giác \[KDOA\] nội tiếp.
Xét tứ giác \[KDOA\], ta có
\[\widehat {KAO} = {90^^\circ }\](Tính chất của tiếp tuyến);
\[\widehat {KDO} = {90^^\circ }\](\[OD \bot BC\] (gt))
Suy ra \[\widehat {KAO} + \widehat {KDO} = {180^^\circ } \Rightarrow \] \[KDOA\] là tứ giác nội tiếp.
b) Đường thẳng \[AE\] cắt \[BC\]tại\[N\]. Chứng minh tam giác \[KNA\]cân và \[K{N^2} = KB.KC\].
![Cho tam giác \[ABC{\rm{ }}(AB < AC)\]có ba góc nhọn, nội tiếp đường tròn tâm (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2025/12/blobid4-1766802992.png)
* Chứng minh tam giác \[KNA\]cân
Ta có \[OD \bot BC\](gt) \[ \Rightarrow D\]là trung điểm của \[BC\](quan hệ vuông góc giữa đường kính và dây) nên \[OD\]là đường trung trực của \[BC\]
mà \[E \in OD\]nên
và \[\widehat {BNA} = \frac{1}{2}\](sđsđ) (góc có đỉnh ở bên trong đường tròn)
\[ \Rightarrow \widehat {KNA} = \frac{1}{2}\](sđsđ) (1)
\[\widehat {EAK} = \frac{1}{2}\]sđ( sđsđ) (2)
Từ (1) và (2) suy ra \[\widehat {EAK} = \widehat {KNA} \Rightarrow \Delta KNA\] cân tại \[K\](đpcm)
* Chứng minh \[K{N^2} = KB.KC\].
Xét \[\Delta KAB\]và \[\Delta KCA\] ta có
\[\widehat {BKA}\]: chung
\[\widehat {KAB} = \widehat {ACK} = \frac{1}{2}\]sđ (cùng chắn cung )
Do đó (g-g)
Nên \[\frac{{KA}}{{KC}} = \frac{{KB}}{{KA}} \Leftrightarrow K{A^2} = KB.KC\]
mà \[\Delta KNA\] cân tại \[K\](cmt) \[ \Rightarrow KA = KN\](3)
Suy ra \[K{N^2} = KB.KC\](đpcm)
c) Kẻ tiếp tuyến \[KM\]của đường tròn \[(O)\](\[M\]là tiếp điểm). Chứng minh tia \[MN\]và tia \[ED\]cắt nhau tại một điểm thuộc đường tròn \[(O)\].
![Cho tam giác \[ABC{\rm{ }}(AB < AC)\]có ba góc nhọn, nội tiếp đường tròn tâm (ảnh 3)](https://video.vietjack.com/upload2/quiz_source1/2025/12/blobid5-1766803040.png)
Cách 1.Ta có: \[\widehat {BMN} = \widehat {KMN} - \widehat {KMB}\]
\[\widehat {CMN} = \widehat {KNM} - \widehat {BCM}\](góc ngoài của tam giác\[MNC\])
Mà \[\widehat {KMN} = \widehat {KNM}\](\[\Delta KMN\]cân do đó \[KM = KN = KA\])
\[\widehat {KMB} = \widehat {BCM}\](cùng chắn )
\[ \Rightarrow \widehat {BMN} = \widehat {CM}N\]
\[ \Rightarrow MN\]là tia phân giác của góc \[BMC\]
+ \[MN\]là tia phân giác của góc \[BMC\] nên \[MN\]đi qua điểm chính giữa \[I\]của
+ \[OE \bot BC\]nên \[ED\]đi qua điểm chính giữa \[I\]của
Vậy tia \[MN\]và tia\[ED\] cắt nhau tại một điểm thược đường tròn tâm \[O\]
Cách 2.Ta có \[A,K,M,D,O\] thuộc đường tròn đường kính \[OK\]
Suy ra \[\widehat {KOM} = \widehat {KDM}\](cùng chắn cung )
Mặt khác \[\widehat {AEM} = \widehat {KOM} \Rightarrow \widehat {AEM} = \widehat {KDM}\]
Suy ra tứ giác \[DEMN\]nội tiếp
Mà \[\widehat {NDE} = {90^ \circ } \Rightarrow \widehat {NME} = {90^ \circ } \Rightarrow MN \bot ME(1)\]
Vẽ đường kính\[EF\], suy ra \[\widehat {FME} = {90^ \circ }\] (góc nội tiếp chắn nửa đường tròn)
\[ \Rightarrow MF \bot ME(2)\]
Từ \[(1),(2)\]suy ra \[M,N,F\]thẳng hàng.
Hay tia \[MN\]và tia\[ED\] cắt nhau tại một điểm thược đường tròn tâm \[O\]