a)Tính \(A = \sqrt 4 + \sqrt {20} - \sqrt 5 - 2\).
b) Cho biểu thức \(B = \left( {\frac{1}{{\sqrt x + 1}} - \frac{1}{{x + \sqrt x }}} \right):\frac{{\sqrt x - 1}}{{{{(\sqrt x + 1)}^2}}}\) với \(x > 0\) và \(x \ne 1\). Rút gọn biểu thức \({\rm{B}}\) và so sánh giá trị của \({\rm{B}\({\rm{m}}\)}\) với 1
a)Tính \(A = \sqrt 4 + \sqrt {20} - \sqrt 5 - 2\).
b) Cho biểu thức \(B = \left( {\frac{1}{{\sqrt x + 1}} - \frac{1}{{x + \sqrt x }}} \right):\frac{{\sqrt x - 1}}{{{{(\sqrt x + 1)}^2}}}\) với \(x > 0\) và \(x \ne 1\). Rút gọn biểu thức \({\rm{B}}\) và so sánh giá trị của \({\rm{B}\({\rm{m}}\)}\) với 1
Quảng cáo
Trả lời:
a)Tính \(A = \sqrt 4 + \sqrt {20} - \sqrt 5 - 2\)
Ta có:
\(\begin{array}{l}A = \sqrt 4 + \sqrt {20} - \sqrt 5 - 2 = \sqrt {{2^2}} + \sqrt {{2^2} \cdot 5} - \sqrt 5 - 2\\\,\,\,\,\, = 2 + 2\sqrt 5 - \sqrt 5 - 2 = (2 - 2) + \left( {2\sqrt 5 - \sqrt 5 } \right) = \sqrt 5 \end{array}\)
Vậy \(A = \sqrt 5 \).
b) Cho biểu thức \(B = \left( {\frac{1}{{\sqrt x + 1}} - \frac{1}{{x + \sqrt x }}} \right):\frac{{\sqrt x - 1}}{{{{(\sqrt x + 1)}^2}}}\) với \(x > 0,x \ne 1\). Rút gọn biểu thúc \(B\) và so sánh giá trị của \(B\) với 1 .
Điều kiện xác định: \(x > 0,x \ne 1\).
\(\begin{array}{l}B = \left( {\frac{1}{{\sqrt x + 1}} - \frac{1}{{\sqrt x \left( {\sqrt x + 1} \right)}}} \right):\frac{{\sqrt x - 1}}{{{{\left( {\sqrt x + 1} \right)}^2}}}\\B = \left( {\frac{{\sqrt x }}{{\sqrt x \left( {\sqrt x + 1} \right)}} - \frac{1}{{\sqrt x \left( {\sqrt x + 1} \right)}}} \right):\frac{{\sqrt x - 1}}{{{{\left( {\sqrt x + 1} \right)}^2}}}\\B = \frac{{\sqrt x - 1}}{{\sqrt x \left( {\sqrt x + 1} \right)}} \cdot \frac{{{{\left( {\sqrt x + 1} \right)}^2}}}{{\sqrt x - 1}} = \frac{{\sqrt x + 1}}{{\sqrt x }}\end{array}\)
Ta có: \(B = \frac{{\sqrt x + 1}}{{\sqrt x }} = 1 + \frac{1}{{\sqrt x }} > 1\,;\,\,\forall x > 0,x \ne 1\).
Vậy với \(x > 0,x \ne 1\) thì \(B = \frac{{\sqrt x + 1}}{{\sqrt x }} > 1\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Cho phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} - 2m + 5 = 0\,\,(*)\), với \(m\) là tham số.
a) Giải phurơng trinh (*) khi \(m = 1\).
Thay \(m = 1\) vào phương trình \((*)\) ta được:
\[{x^2} - 2\left( {1 + 1} \right)x + 1 - 2 + 5 = 0 \Leftrightarrow {x^2} - 4x + 4 = 0\]\[ \Leftrightarrow {\left( {x - 2} \right)^2} = 0 \Leftrightarrow x - 2 = 0 \Leftrightarrow x = 2\]
Vậy khi \({\rm{m}} = 1\) phương trình có nghiệm duy nhất \(x = 2\).
b) Tìm tất cả các giá trị của tham số m để phương trình (*) có hai nghiệm phân biệt \({x_1},{x_2}\) thoả mãn \(\sqrt {4x_1^2 + 4m{x_1} + {m^2}} + \sqrt {x_2^2 + 4m{x_2} + 4{m^2}} = 7m + 2.\)
Ta có: \(\Delta ' = {(m + 1)^2} - \left( {{m^2} - 2m + 5} \right) = {m^2} + 2m + 1 - {m^2} + 2m - 5 = 4m - 4\)
Để phương trình (*) có 2 nghiệm phân biệt \({x_1},{x_2}\) thì \(\Delta ' > 0 \Leftrightarrow 4m - 4 > 0 \Leftrightarrow m > 1\).
Theo đề cho: \(\sqrt {4x_1^2 + 4m{x_1} + {m^2}} + \sqrt {x_2^2 + 4m{x_2} + 4{m^2}} = 7m + 2\)
\( \Leftrightarrow \sqrt {{{\left( {2{x_1} + m} \right)}^2}} + \sqrt {{{\left( {{x_2} + 2m} \right)}^2}} = 7m + 2\)
\( \Leftrightarrow \left| {2{x_1} + m} \right| + \left| {{x_2} + 2m} \right| = 7m + 2\)
Áp dụng định lí Vi-ét ta có: \[\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = 2\left( {m + 1} \right) = 2m + 2 > 0\,\,\,\left( {{\rm{do }}m > 1} \right)}\\{{x_1}{x_2} = {m^2} - 2m + 5 = {{\left( {m - 1} \right)}^2} + 4 > 0\,\,\forall m}\end{array}} \right.\]
\[ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_1} > 0}\\{{x_2} > 0}\end{array}\,\,\,\,\forall m > 1 \Rightarrow \left\{ {\begin{array}{*{20}{l}}{2{x_1} + m > 0}\\{{x_2} + 2m > 0}\end{array}\,\,\,\,\,\forall m} \right.} \right. > 1\]
Khi đó ta có: \(\left| {2{x_1} + m} \right| + \left| {{x_2} + 2m} \right| = 7m + 2 \Leftrightarrow 2{x_1} + m + {x_2} + 2m = 7m + 2\)
\(\begin{array}{l} \Leftrightarrow 2{x_1} + {x_2} = 4m + 2 \Leftrightarrow 2m + 2 + {x_1} = 4m + 2\\ \Leftrightarrow {x_1} = 2m \Rightarrow {x_2} = 2m + 2 - {x_1} = 2\\ \Rightarrow {x_1}{x_2} = 4m = {m^2} - 2m + 5 \Leftrightarrow {m^2} - 6m + 5 = 0\end{array}\)
Ta có \(a + b + c = 1 - 6 + 5 = 0\) nên phương trình có 2 nghiệm phân biệt \(\left[ {\begin{array}{*{20}{l}}{{m_1} = 1\,\,(ktm)}\\{{m_2} = 5\,\,(tm)}\end{array}} \right.\)
Vậy \(m = 5\) thoả mãn yêu cầu bài toán
Lời giải
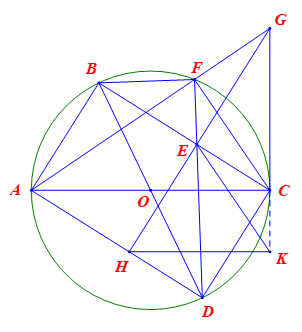
a) Chứng minh rằng \(AB = CD\) và \(\widehat {CFD} = \widehat {BCA}\).
· Chứng \({\mathop{\rm minh}\nolimits} AB = CD\)
Xét tam giác \({\rm{AOB}}\) và tam giác \[COD\] có:
\(OA = OC\,\,\left( { = R} \right)\)
\(\widehat {{O_1}} = \widehat {{O_2}}\)(đối đỉnh)
\(OB = OD\,\,\left( {\, = R} \right)\)
\( \Rightarrow \Delta AOB = \Delta COD\,\,(c \cdot g \cdot c)\)
\( \Rightarrow {\rm{AB}} = {\rm{CD}}\) (2 cạnh tương ứng) (đp̣cm)
Chứng minh \(\widehat {CFD} = \widehat {BCA}\)
Ta có: \(\widehat {CFD} = \widehat {CBD}\) (hai góc nội tiếp cùng góc chắn cung \({\rm{CD}}\) ).
Lại có: cân tại \(O\)\( \Rightarrow \widehat {OBC} = \widehat {OCB}\) (tính chất tam giác cân)
\( \Rightarrow \widehat {CBD} = \widehat {BCA}\)
Vậy \(\widehat {CFD} = \widehat {BCA}\).
b) Đường thẳng qua E vuông góc với \(BC\)cắt tia \(AF\)tại\(G\). Chứng minh rằng tứ giác CEFG nội tiếp và\(CD.EG = CB \cdot CE\)
· Chứng minh tứ giác CEFG nôi tiếp
Ta có: \(\widehat {AFC} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow \widehat {CFG} = 90^\circ \)
Xét tứ giác \({\rm{CEFG}}\) có: \(\widehat {CFG} = \widehat {CEG} = 90^\circ \).
Mà hai đỉnh \({\rm{E}},{\rm{F}}\) kề nhau cùng nhìn dưới \({\rm{CG}}\) dưới hai góc bằng nhau
\( \Rightarrow \) Tứ giác EFGC nội tiếp (dhnb) (đpcm)
· Chứng minh \[CD.EG = CB.CE\]
Ta có: .
Xét tam giác \({\rm{AGC}}\) và tam giác \({\rm{ACF}}\) có:
\( \Rightarrow \widehat {ACG} = \widehat {AFC} = 90^\circ \) (2 góc tương ứng)
\( \Rightarrow CG \bot AC \Rightarrow {\rm{CG}}\) là tiếp tuyến của đường trong \(({\rm{O}})\) tại \(C\)
\( \Rightarrow {\rm{CG}}\) là tiếp tuyến của đường trong \(({\rm{O}})\) tại \({\rm{C}}\).
Xét tam giác \({\rm{BCD}}\) và tam giác \({\rm{GEC}}\) có:
\(\widehat {BCD} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \widehat {BCD} = \widehat {GEC} = 90^\circ \).
\(\widehat {BDC} = \widehat {GCE}\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn ).
\( \Rightarrow \frac{{CB}}{{CD}} = \frac{{EG}}{{CE}} \Rightarrow CD \cdot EG = CB \cdot CE\) (đpcm)
c) Gọi \(H\)là giao điểm của tia \(GE\)và\(AD\). Đường thẳng qua\(H\), song song với \(AC\)cắt dường thẳng qua\(E\), song song với \(FC\) tại \[K\]. Chứng minh rằng ba điểm \(G\,,\,\,C\,,\,\,K\)thẳng hàng.
Vì \(CEFG\)là tứ giác nội tiếp (cmt)
\( \Rightarrow \widehat {EGC} = \widehat {EFC} = \widehat {DFC}\) (hai góc nội tiếp cùng chắn cung\(EC\))
Mà \(\widehat {DFC = }\widehat {DAC}\) (hai góc nội tiếp cùng chắn cung \({\rm{CD}}\) )
\( \Rightarrow \widehat {EGC} = \widehat {DAC} \Rightarrow \widehat {HGC} = \widehat {HAC}{\rm{ }}\)
Mà hai đinh \({\rm{A}},{\rm{G}}\) kề nhau cùng nhìn \({\rm{HC}}\) dưới hai góc bằng nhau.
\( \Rightarrow AGCH\) là tứ giác nội tiếp (dhnb).
\( \Rightarrow \widehat {AGH} = \widehat {ACH} = \widehat {FGE}\) (hai góc nội tiếp cùng chắn cung \({\rm{AH}}\)).
Mà \({\rm{CEFG}}\) là tứ giác nội tiếp \( \Rightarrow \widehat {FGE} = \widehat {FCE}\) (hai góc nội tiếp cùng chắn cung \({\rm{EF}}\)).
\( \Rightarrow \widehat {ACH} = \widehat {FCE}\)
\({\rm{Ta}}\) có: \({\rm{EK}}\,{\rm{//}}\,\,{\rm{FC}}\,\,({\rm{gt}}) \Rightarrow \widehat {FCE} = \widehat {CEK}\) (so le trong)
\({\rm{HK}}\,\,{\rm{//}}\,\,{\rm{AC (gt) }} \Rightarrow \widehat {ACH} = \widehat {CHK}{\rm{ (so le trong) }}\)
\( \Rightarrow \widehat {CEK} = \widehat {CHK}\)Mà hai đinh \({\rm{E}},{\rm{H}}\) kề nhau củng nhìn \({\rm{CK}}\) dưới hai góc bằng nhau
\( \Rightarrow CEHK\) là tứ giác nội tiếp (dhnb).
\( \Rightarrow \widehat {HEC} + \widehat {HKC} = 180^\circ {\rm{ }}\)
Mà \(\widehat {HEC} = 90^\circ \) (do \(GH \bot BC\) tại \({\rm{E}}\) ) \( \Rightarrow \widehat {HKC} = 90^\circ \Rightarrow CK \bot HK\).
Mà \({\rm{HK}}//{\rm{AC}}({\rm{gt}}) \Rightarrow CK \bot AC\) (từ vuông góc đến song song).
Mà \(CG \bot AC\,\,\,(cmt)\).
Vậy \({\rm{G}},{\rm{C}},{\rm{K}}\) thẳng hàng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.