$\begin{array}{l}A = \sqrt 4 + \sqrt {20} - \sqrt 5 - 2 = \sqrt {{2^2}} + \sqrt {{2^2} \cdot 5} - \sqrt 5 - 2\\\,\,\,\,\, = 2 + 2\sqrt 5 - \sqrt 5 - 2 = (2 - 2) + \left( {2\sqrt 5 - \sqrt 5 } \right) = \sqrt 5 \end{array}$

Vậy $A = \sqrt 5 $.

b) Cho biểu thức $B = \left( {\frac{1}{{\sqrt x + 1}} - \frac{1}{{x + \sqrt x }}} \right):\frac{{\sqrt x - 1}}{{{{(\sqrt x + 1)}^2}}}$ với $x > 0,x \ne 1$. Rút gọn biểu thúc $B$ và so sánh giá trị của $B$ với 1 .

Điều kiện xác định: $x > 0,x \ne 1$.

$\begin{array}{l}B = \left( {\frac{1}{{\sqrt x + 1}} - \frac{1}{{\sqrt x \left( {\sqrt x + 1} \right)}}} \right):\frac{{\sqrt x - 1}}{{{{\left( {\sqrt x + 1} \right)}^2}}}\\B = \left( {\frac{{\sqrt x }}{{\sqrt x \left( {\sqrt x + 1} \right)}} - \frac{1}{{\sqrt x \left( {\sqrt x + 1} \right)}}} \right):\frac{{\sqrt x - 1}}{{{{\left( {\sqrt x + 1} \right)}^2}}}\\B = \frac{{\sqrt x - 1}}{{\sqrt x \left( {\sqrt x + 1} \right)}} \cdot \frac{{{{\left( {\sqrt x + 1} \right)}^2}}}{{\sqrt x - 1}} = \frac{{\sqrt x + 1}}{{\sqrt x }}\end{array}$

Ta có: $B = \frac{{\sqrt x + 1}}{{\sqrt x }} = 1 + \frac{1}{{\sqrt x }} > 1\,;\,\,\forall x > 0,x \ne 1$.

Vậy với $x > 0,x \ne 1$ thì $B = \frac{{\sqrt x + 1}}{{\sqrt x }} > 1$.

Câu 2

Cho hàm số ${\rm{y}} = \frac{1}{2}{{\rm{x}}^2}$ có đồ thị $({\rm{P}})$.

a)     Vẽ đồ thị (P).

b)     Đường thằng ${\rm{y}} = - {\rm{x}} + {\rm{b}}$ (với ${\rm{b}} > 0$ ) lần lượt cắt các tia ${\rm{Ox}},{\rm{Oy}}$ tại ${\rm{E}},{\rm{F}}$. Chứng minh rằng tam giác ${\rm{OEF}}$ vuông cân và tìm ${\rm{b}}$ đề tâm của đường tròn ngoại tiếp tam giác ${\rm{OEF}}$ là một điểm thuộc $({\rm{P}})$, với ${\rm{O}}$ là gốc tọa độ.

Xem đáp án

Lời giải

Cho hàm số ${\rm{y}} = \frac{1}{2}{{\rm{x}}^2}$ có đồ thị $({\rm{P}})$.

a) Vẽ đồ thị (P).

Ta có bảng giá trị sau:

$x$	$ - 2$	$ - 1$	$0$	$1$	$2$
$y = \frac{1}{2}{x^2}$	$2$	$\frac{1}{2}$	$0$	$\frac{1}{2}$	$2$

$ \Rightarrow $ Đồ thị hàm số là đường cong parabol đi qua các điểm

$O\,\left( {0\,;\,\,0} \right)\,;\,\,A\,\left( { - 2\,;\,\,2} \right)\,;\,\,\,B\,\left( { - 1\,;\,\,\frac{1}{2}} \right)\,\,;\,\,\,C\,\,\left( {1\,;\,\,\frac{1}{2}} \right)\,\,;\,\,D\,\left( {2\,;\,\,2} \right)$

Hệ số $a = \frac{1}{2} > 0$ nên parabol có bề cong hướng xuống. Đồ thị hàm số nhận ${\rm{Oy}}$ làm trục đối xứng.

Ta vẽ được đồ thị hàm số $y = \frac{1}{2}{x^2}$ như sau:

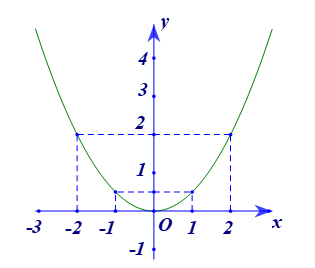
Cho hàm số y = 1/2 x ^2 có đồ thị (P) (ảnh 1)

a) Đường thẳng $y = - x + b$ (với $b > 0$) lần lượt cắt \[Ox,\]\[Oy\] tại $E\,,\,\,F$. Chứng minh rằng tam giác $OEF$vuông cân và tìm $b$ để tâm đuờng tròn ngoại tiếp tam giác \[OEF\] là gốc tọa độ.

Cho $y = 0 \Rightarrow - x + b = 0 \Leftrightarrow x = b$

$ \Rightarrow $ Đường thẳng $y = - x + b$ cắt ${\rm{Ox}}$ tại ${\rm{E}}({\rm{b}};0)$.

Cho $x = 0 \Rightarrow y = 0 + b = b$

$ \Rightarrow $ Đường thẳng $y = - x + b$ cắt ${\rm{Oy}}$ tại ${\rm{F}}(0;{\rm{b}})$.

Xét $\Delta OEF$ có: $\left\{ {\begin{array}{*{20}{l}}{OE \bot OF\,\,\,\left( {{\rm{do }}Ox \bot Oy} \right)}\\{OE = OF = b\,\,\,\left( {{\rm{do }}b > 0} \right)}\end{array} \Rightarrow \Delta OEF} \right.$ vuông cân tại ${\rm{O}}$.

$ \Rightarrow $ Tâm đường tròn ngoại tiếp $\Delta OEF$ là trung điểm cạnh huyền \[EF\].

Gọi tâm đường tròn ngoại tiếp $\Delta OEF$ là $H$.

Gọi $M,\,\,N$ lần lượt là hình chiếu của $H$ lên $Ox\,,\,\,Oy$.

Ta có $\left\{ {\begin{array}{*{20}{l}}{HM \bot Ox}\\{OF \bot Ox}\end{array} \Rightarrow HM\,{\rm{//}}\,OF} \right.$ (từ vuông góc đến song song).

Mà $H$ là trung điểm của $EF$$ \Rightarrow M$ là trung điểm của $OE$ (Tính chất đường trung bình của tam giác).

$ \Rightarrow HM$ là đường trung bình của tam giác $OEF \Rightarrow HM = \frac{1}{2}OF = \frac{b}{2}$.

Chứng minh tương tự ta tính được $HN = \frac{b}{2}$$ \Rightarrow H\left( {\frac{b}{2};\frac{b}{2}} \right)$

Để tâm đường tròn ngoại tiếp tam giác $OEF$ là một điểm thuộc $({\rm{P}}) \Leftrightarrow H\left( {\frac{b}{2};\frac{b}{2}} \right) \in (P)$.

\[\begin{array}{l} \Leftrightarrow \frac{b}{2} = \frac{1}{2} \cdot {\left( {\frac{b}{2}} \right)^2} \Leftrightarrow \frac{b}{2} = \frac{{{b^2}}}{8} \Leftrightarrow {b^2} - 4b = 0\\ \Leftrightarrow b\left( {b - 4} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}b = 0\,\,\,(L)\\b = 4\,\,(TM)\end{array} \right.\,\,\end{array}\]

Vậy $b = 4$ là giá trị cần tìm.

Câu 3

a) Tổng của hai số bằng 23. Hai lần số này lớn hơn số kia 1 đơn vị. Tìm hai số đó.

b) Hai đội công nhân cùng dọn vệ sinh khu vực khán đài Lễ hội Pháo hoa quốc tế Đà Nã̃ng trong 1 giờ 12 phút thì xong. Nếu đội ${\rm{A}}$ làm 40 phút và đội ${\rm{B}}$ làm 2 giờ thì xong việc. Hỏi nếu làm riêng thì mỗi đội hoàn thành công việc trong bao lâu?

Xem đáp án

Lời giải

a) Tổng của hai số bằng 23. Hai lần số này hơn số kia 1 đơn vị. Tim hai số đó.

Gọi số thứ nhất là ${\rm{a}}$, số thứ hai là ${\rm{b}}$.

Theo đề bài:

Tổng của hai số bằng 23 , ta có phương trình: ${\rm{a}} + {\rm{b}} = 23$;

Hai lần số này hơn số kia 1 đơn vị, ta có phương trình: $2{\rm{a}} - {\rm{b}} = 1$.

Theo bài ra ta có hệ phương trình: $\left\{ {\begin{array}{*{20}{l}}{a + b = 23}\\{2a - b = 1}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a + b = 23}\\{3a = 24}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a + b = 23}\\{a = 8}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 8}\\{b = 15}\end{array}} \right.} \right.} \right.} \right.$

Vậy số thứ nhất là 8 , số thứ hai là 15 .

b) Đổi 1 giờ 12 phút $ = \frac{6}{5}\;{\rm{h}};40$ phút $ = \frac{2}{3}\;{\rm{h}}$

Gọi thời gian đội ${\rm{A}}$ làm riêng hoàn thành công việc là ${\rm{x}}({\rm{h}})\,,\,\,\,\left( {x > \frac{6}{5}} \right)$

Thời gian đội ${\rm{B}}$ làm riêng hoàn thành công việc là ${\rm{y}}({\rm{h}})\,;\,\,\,\left( {y > \frac{6}{5}} \right)$

Trong 1 giờ, đội ${\rm{A}}$ làm được $\frac{1}{x}$ công việc; đội ${\rm{B}}$ làm được $\frac{1}{y}$ công việc.

$ \Rightarrow $Trong 1 giờ hai đội cùng làm được $\frac{1}{x} + \frac{1}{y}$ (công việc)

Theo đề bài, hai đội làm cùng nhau thì sau 1 giờ 12 phút $ = \frac{6}{5}\;{\rm{h}}$ xong công việc nên ta có phương trình: $\frac{6}{5} \cdot \left( {\frac{1}{x} + \frac{1}{y}} \right) = 1 \Leftrightarrow \frac{1}{x} + \frac{1}{y} = \frac{5}{6}$

Theo đề bài, nếu đội ${\rm{A}}$ làm 40 phút $ = \frac{2}{3}\;{\rm{h}}$ và đội ${\rm{B}}$ làm 2 giờ thì xong công việc nên ta có phương trình: $\frac{2}{{3x}} + \frac{2}{y} = 1$

Ta có hệ phương trình: $\left\{ {\begin{array}{*{20}{l}}{\frac{1}{x} + \frac{1}{y} = \frac{5}{6}}\\{\frac{2}{{3x}} + \frac{2}{y} = 1}\end{array}} \right.$.

Đặt\[\left\{ \begin{array}{l}u = \frac{1}{x}\\v = \frac{1}{y}\end{array} \right.\] Hệ phương trình trở thành

\[\left\{ {\begin{array}{*{20}{l}}{u + v = \frac{5}{6}}\\{\frac{2}{3}u + 2v = 1}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{v = \frac{5}{6} - u}\\{\frac{2}{3}u + 2v = 1}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{v = \frac{5}{6} - u}\\{\frac{2}{3}u + 2\left( {\frac{5}{6} - u} \right) = 1}\end{array}} \right.} \right.} \right.\]\[ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{v = \frac{5}{6} - u}\\{\frac{2}{3}u + \frac{5}{3} - 2u = 1}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{v = \frac{5}{6} - u}\\{\frac{4}{3}u = \frac{2}{3}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{v = \frac{5}{6} - u}\\{u = \frac{1}{2}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{v = \frac{1}{3}}\\{u = \frac{1}{2}}\end{array}} \right.} \right.} \right.} \right. \Rightarrow \left\{ {\begin{array}{*{20}{l}}{\frac{1}{x} = \frac{1}{2}}\\{\frac{1}{y} = \frac{1}{3}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 2}\\{y = 3}\end{array}} \right.} \right.{\rm{ }}\]

Vậy thời gian đội ${\rm{A}}$ làm riêng hoàn thành công việc là 2 giờ; thời gian đội ${\rm{B}}$ làm riêng hoàn thành công việc là 3 giờ.

Câu 4

Cho phương trình ${{\rm{x}}^2} - 2\left( {{\rm{m}} + 1} \right){\rm{x}} + {{\rm{m}}^2} - 2\;{\rm{m}} + 5 = 0\,\,\,\,()$, với là tham số.

a) Giải phương trình $()$ khi ${\rm{m}} = 1$.

b) Tìm tất cả các giá trị của tham số ${\rm{m}}$ để phương trình (*) có hai nghiệm phân biệt ${x_1},{x_2}$ thỏa mãn $\sqrt {4x_1^2 + 4m{x_1} + {m^2}} + \sqrt {x_2^2 + 4{\rm{m}}{{\rm{x}}_2} + 4\;{{\rm{m}}^2}} = 7\;{\rm{m}} + 2$.

Xem đáp án

Lời giải

Cho phương trình ${x^2} - 2\left( {m + 1} \right)x + {m^2} - 2m + 5 = 0\,\,(*)$, với $m$ là tham số.

a) Giải phurơng trinh (*) khi $m = 1$.

Thay $m = 1$ vào phương trình $(*)$ ta được:

\[{x^2} - 2\left( {1 + 1} \right)x + 1 - 2 + 5 = 0 \Leftrightarrow {x^2} - 4x + 4 = 0\]\[ \Leftrightarrow {\left( {x - 2} \right)^2} = 0 \Leftrightarrow x - 2 = 0 \Leftrightarrow x = 2\]

Vậy khi ${\rm{m}} = 1$ phương trình có nghiệm duy nhất $x = 2$.

b) Tìm tất cả các giá trị của tham số m để phương trình (*) có hai nghiệm phân biệt ${x_1},{x_2}$ thoả mãn $\sqrt {4x_1^2 + 4m{x_1} + {m^2}} + \sqrt {x_2^2 + 4m{x_2} + 4{m^2}} = 7m + 2.$

Ta có: $\Delta ' = {(m + 1)^2} - \left( {{m^2} - 2m + 5} \right) = {m^2} + 2m + 1 - {m^2} + 2m - 5 = 4m - 4$

Để phương trình (*) có 2 nghiệm phân biệt ${x_1},{x_2}$ thì $\Delta ' > 0 \Leftrightarrow 4m - 4 > 0 \Leftrightarrow m > 1$.

Theo đề cho: $\sqrt {4x_1^2 + 4m{x_1} + {m^2}} + \sqrt {x_2^2 + 4m{x_2} + 4{m^2}} = 7m + 2$

$ \Leftrightarrow \sqrt {{{\left( {2{x_1} + m} \right)}^2}} + \sqrt {{{\left( {{x_2} + 2m} \right)}^2}} = 7m + 2$

$ \Leftrightarrow \left| {2{x_1} + m} \right| + \left| {{x_2} + 2m} \right| = 7m + 2$

Áp dụng định lí Vi-ét ta có: \[\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = 2\left( {m + 1} \right) = 2m + 2 > 0\,\,\,\left( {{\rm{do }}m > 1} \right)}\\{{x_1}{x_2} = {m^2} - 2m + 5 = {{\left( {m - 1} \right)}^2} + 4 > 0\,\,\forall m}\end{array}} \right.\]

\[ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_1} > 0}\\{{x_2} > 0}\end{array}\,\,\,\,\forall m > 1 \Rightarrow \left\{ {\begin{array}{*{20}{l}}{2{x_1} + m > 0}\\{{x_2} + 2m > 0}\end{array}\,\,\,\,\,\forall m} \right.} \right. > 1\]

Khi đó ta có: $\left| {2{x_1} + m} \right| + \left| {{x_2} + 2m} \right| = 7m + 2 \Leftrightarrow 2{x_1} + m + {x_2} + 2m = 7m + 2$

$\begin{array}{l} \Leftrightarrow 2{x_1} + {x_2} = 4m + 2 \Leftrightarrow 2m + 2 + {x_1} = 4m + 2\\ \Leftrightarrow {x_1} = 2m \Rightarrow {x_2} = 2m + 2 - {x_1} = 2\\ \Rightarrow {x_1}{x_2} = 4m = {m^2} - 2m + 5 \Leftrightarrow {m^2} - 6m + 5 = 0\end{array}$

Ta có $a + b + c = 1 - 6 + 5 = 0$ nên phương trình có 2 nghiệm phân biệt $\left[ {\begin{array}{*{20}{l}}{{m_1} = 1\,\,(ktm)}\\{{m_2} = 5\,\,(tm)}\end{array}} \right.$

Vậy $m = 5$ thoả mãn yêu cầu bài toán

Câu 5

Cho đường tròn $(O)$ có hai đường kính $AC,\,\,BD$ ($A$khác $B,\,D$). Trên đoạn thẳng $BC$ lấy điểm $E$ ($E$ khác$B,\,\,C$), đường thẳng $ED$ cắt đường tròn $(O)$ tại điểm thứ hai là$F$.

a)     Chứng minh rằng $AB = CD$ và $\widehat {CFD} = \widehat {BCA}$.

b)     Đường thẳng qua $E$, vuông góc với $BC$ cắt tia $AF$ tại $G$. Chứng minh rằng tứ giác $CEFG$ nội tiếp và $CD.EG = CB.CE$.

c)     Gọi $H$ là giao điểm của tia $GE$ và $AD$. Đường thẳng qua $H$, song song với $AC$ cắt đường thẳng qua$E$, song song với $FC$ tại $K$. Chứng minh rằng ba điểm $G,\,C,\,K$ thẳng hàng.

Xem đáp án

Lời giải

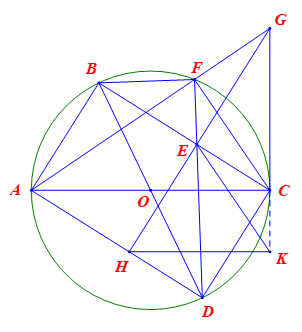
$Cho đường tròn $(O)$ có hai đường kính $AC,\,\,BD$ ($A$khác $B,\,D$). Trên đoạn thẳng (ảnh 1)$

a) Chứng minh rằng $AB = CD$ và $\widehat {CFD} = \widehat {BCA}$.

· Chứng ${\mathop{\rm minh}\nolimits} AB = CD$

Xét tam giác ${\rm{AOB}}$ và tam giác \[COD\] có:

$OA = OC\,\,\left( { = R} \right)$

$\widehat {{O_1}} = \widehat {{O_2}}$(đối đỉnh)

$OB = OD\,\,\left( {\, = R} \right)$

$ \Rightarrow \Delta AOB = \Delta COD\,\,(c \cdot g \cdot c)$

$ \Rightarrow {\rm{AB}} = {\rm{CD}}$ (2 cạnh tương ứng) (đp̣cm)

Chứng minh $\widehat {CFD} = \widehat {BCA}$

Ta có: $\widehat {CFD} = \widehat {CBD}$ (hai góc nội tiếp cùng góc chắn cung ${\rm{CD}}$ ).

Lại có: cân tại $O$$ \Rightarrow \widehat {OBC} = \widehat {OCB}$ (tính chất tam giác cân)

$ \Rightarrow \widehat {CBD} = \widehat {BCA}$

Vậy $\widehat {CFD} = \widehat {BCA}$.

b) Đường thẳng qua E vuông góc với $BC$cắt tia $AF$tại$G$. Chứng minh rằng tứ giác CEFG nội tiếp và$CD.EG = CB \cdot CE$

· Chứng minh tứ giác CEFG nôi tiếp

Ta có: $\widehat {AFC} = 90^\circ $ (góc nội tiếp chắn nửa đường tròn)

$ \Rightarrow \widehat {CFG} = 90^\circ $

Xét tứ giác ${\rm{CEFG}}$ có: $\widehat {CFG} = \widehat {CEG} = 90^\circ $.

Mà hai đỉnh ${\rm{E}},{\rm{F}}$ kề nhau cùng nhìn dưới ${\rm{CG}}$ dưới hai góc bằng nhau

$ \Rightarrow $ Tứ giác EFGC nội tiếp (dhnb) (đpcm)

· Chứng minh \[CD.EG = CB.CE\]

Ta có: $\hat{A G C} = \frac{1}{2} (s ñ \overset{⏜}{A C} - s ñ \overset{⏜}{C F}) = \frac{1}{2} s ñ \overset{⏜}{A F} = \hat{A C F}$ .

Xét tam giác ${\rm{AGC}}$ và tam giác ${\rm{ACF}}$ có:

$ \Rightarrow \widehat {ACG} = \widehat {AFC} = 90^\circ $ (2 góc tương ứng)

$ \Rightarrow CG \bot AC \Rightarrow {\rm{CG}}$ là tiếp tuyến của đường trong $({\rm{O}})$ tại $C$

$ \Rightarrow {\rm{CG}}$ là tiếp tuyến của đường trong $({\rm{O}})$ tại ${\rm{C}}$.

Xét tam giác ${\rm{BCD}}$ và tam giác ${\rm{GEC}}$ có:

$\widehat {BCD} = 90^\circ $ (góc nội tiếp chắn nửa đường tròn) $ \Rightarrow \widehat {BCD} = \widehat {GEC} = 90^\circ $.

$\widehat {BDC} = \widehat {GCE}$ (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn ).

$ \Rightarrow \frac{{CB}}{{CD}} = \frac{{EG}}{{CE}} \Rightarrow CD \cdot EG = CB \cdot CE$ (đpcm)

c) Gọi $H$là giao điểm của tia $GE$và$AD$. Đường thẳng qua$H$, song song với $AC$cắt dường thẳng qua$E$, song song với $FC$ tại \[K\]. Chứng minh rằng ba điểm $G\,,\,\,C\,,\,\,K$thẳng hàng.

Vì $CEFG$là tứ giác nội tiếp (cmt)

$ \Rightarrow \widehat {EGC} = \widehat {EFC} = \widehat {DFC}$ (hai góc nội tiếp cùng chắn cung$EC$)

Mà $\widehat {DFC = }\widehat {DAC}$ (hai góc nội tiếp cùng chắn cung ${\rm{CD}}$ )

$ \Rightarrow \widehat {EGC} = \widehat {DAC} \Rightarrow \widehat {HGC} = \widehat {HAC}{\rm{ }}$

Mà hai đinh ${\rm{A}},{\rm{G}}$ kề nhau cùng nhìn ${\rm{HC}}$ dưới hai góc bằng nhau.

$ \Rightarrow AGCH$ là tứ giác nội tiếp (dhnb).

$ \Rightarrow \widehat {AGH} = \widehat {ACH} = \widehat {FGE}$ (hai góc nội tiếp cùng chắn cung ${\rm{AH}}$).

Mà ${\rm{CEFG}}$ là tứ giác nội tiếp $ \Rightarrow \widehat {FGE} = \widehat {FCE}$ (hai góc nội tiếp cùng chắn cung ${\rm{EF}}$).

$ \Rightarrow \widehat {ACH} = \widehat {FCE}$

${\rm{Ta}}$ có: ${\rm{EK}}\,{\rm{//}}\,\,{\rm{FC}}\,\,({\rm{gt}}) \Rightarrow \widehat {FCE} = \widehat {CEK}$ (so le trong)

${\rm{HK}}\,\,{\rm{//}}\,\,{\rm{AC (gt) }} \Rightarrow \widehat {ACH} = \widehat {CHK}{\rm{ (so le trong) }}$

$ \Rightarrow \widehat {CEK} = \widehat {CHK}$Mà hai đinh ${\rm{E}},{\rm{H}}$ kề nhau củng nhìn ${\rm{CK}}$ dưới hai góc bằng nhau

$ \Rightarrow CEHK$ là tứ giác nội tiếp (dhnb).

$ \Rightarrow \widehat {HEC} + \widehat {HKC} = 180^\circ {\rm{ }}$

Mà $\widehat {HEC} = 90^\circ $ (do $GH \bot BC$ tại ${\rm{E}}$ ) $ \Rightarrow \widehat {HKC} = 90^\circ \Rightarrow CK \bot HK$.

Mà ${\rm{HK}}//{\rm{AC}}({\rm{gt}}) \Rightarrow CK \bot AC$ (từ vuông góc đến song song).

Mà $CG \bot AC\,\,\,(cmt)$.

Vậy ${\rm{G}},{\rm{C}},{\rm{K}}$ thẳng hàng.

\(x\)	\( - 2\)	\( - 1\)	\(0\)	\(1\)	\(2\)
\(y = \frac{1}{2}{x^2}\)	\(2\)	\(\frac{1}{2}\)	\(0\)	\(\frac{1}{2}\)	\(2\)

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Tiếng Anh

Giáo dục Kinh tế và Pháp luật

ĐHQG Hồ Chí Minh

ĐH Bách Khoa

ĐHQG Hà Nội

Bộ Công an

ĐHSP Hà Nội

Bằng lái xe

English Test

IT Test

Đại học

Viên chức

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Công nghệ

Tin học

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Công nghệ

Tin học

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Global success

iLearn Smart World

Friends Global

Bright

Explore new worlds

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Toán

Vật lý

Hóa học