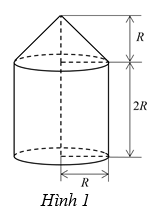
Một chi tiết máy gồm một phần có dạng hình trụ, phần còn lại có dạng hình nón với các kích thước như hình 1. Biết rằng phần hình trụ có chu vi đáy là \[37,68\,{\rm{cm}}.\] Tính thể tích của chi tiết máy đó (lấy \(\pi  \approx 3,14{\rm{;}}\) kết quả làm tròn đến chữ số thập phân thứ 2).

a. (1,0 điểm)

  \(A = 6\sqrt 2  - 5\sqrt 2  - \left| {\sqrt 2  - 1} \right|\)

     \( = \sqrt 2  - \sqrt 2  + 1\) (vì \(\sqrt 2  - 1 > 0\)) \[ = 1\]

 Với \[x\; \ge 0,\,\,x \ne 4,\;\,x \ne 9\] ta có :

  \[B = \left[ {\frac{{3\left( {\sqrt x  + 2} \right)}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}} + \frac{{\sqrt x }}{{\sqrt x  - 2}}} \right]:\frac{{\left( {\sqrt x  - 3} \right)\left( {\sqrt x  + 3} \right)}}{{\sqrt x  - 3}}\]

    \( = \frac{{3 + \sqrt x }}{{\sqrt x  - 2}} \cdot \frac{1}{{\sqrt x  + 3}} = \frac{1}{{\sqrt x  - 2}}.\)

b. (0,5 điểm)

Để \(A - 2B = 3\) \( \Leftrightarrow 1 - \frac{2}{{\sqrt x  - 2}} = 3 \Rightarrow \sqrt x  - 2 - 2 = 3\sqrt x  - 6 \Leftrightarrow 2\sqrt x  = 2 \Leftrightarrow \sqrt x  = 1\)

\( \Leftrightarrow x = 1\) (thoả mãn).

Vậy \(x = 1\) thì \(A - 2B = 3.\)

1a)Với \(m =  - 3\) phương trình \(\left( 1 \right)\) có dạng \({x^2} + 8x = 0.\)

\[ \Leftrightarrow x{\rm{(}}x + 8{\rm{)}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x + 8 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x =  - 8\end{array} \right.\]

Vậy khi \(m =  - 3,\) phương trình có nghiệm là \(x = 0;\,\,x =  - 8.\)

b)Có \(\Delta ' = {\left[ { - \left( {m - 1} \right)} \right]^2} - {m^2} + 9 = {m^2} - 2m + 1 - {m^2} + 9 =  - 2m + 10.\)

Phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) \[ \Leftrightarrow \Delta ' > 0 \Leftrightarrow  - 2m + 10 > 0 \Leftrightarrow m < 5\]

Theo hệ thức Vi-ét \[\left\{ \begin{array}{l}{x_1} + {x_2} = 2\left( {m - 1} \right)\,\,\,\,\,\left( 2 \right)\\{x_1}{x_2} = {m^2} - 9\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 3 \right)\end{array} \right.\] 

Theo đề bài ta có: \[{x_1} - {x_2} = 2m - 10,\] kết hợp với (2) ta được \[{x_1} = 2m - 6;{x_2} = 4\]  

Thay \[{x_1} = 2m - 6;{x_2} = 4\] vào (3) ta được:\(\left( {2m - 6} \right)4 = {m^2} - 9 \Leftrightarrow {m^2} - 8m + 15 = 0\).

Giải được \(m = 3\) (thoả mãn), \(m = 5\) (loại)

Vậy với \(m = 3\) phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn

\({x_1} - {x_2} = 2m - 10.\)

2.Gọi chiều dài của vườn ban đầu là \[x\left( m \right)\], chiều rộng của vườn ban đầu là \[y\left( m \right)\]

(ĐK: \(0 < y < x < 50\))

Vì chu vi của vườn ban đầu là \[100m\] nên ta có phương trình:

\[2\left( {x + y} \right) = 100 \Leftrightarrow x + y = 50{\rm{ }}\left( 1 \right)\]

Chiều dài của vườn sau khi mở rộng là: \[\left( {x + 5} \right){\rm{ }}\left( m \right)\]

Chiều rộng của vườn sau khi mở rộng là: \[\left( {y + 4} \right){\rm{ }}\left( m \right)\]

Khi đó diện tích vườn trường đã tăng thêm \[240{m^2}\] nên ta có phương trình:

\(\left( {x + 5} \right)\left( {y + 4} \right) - xy = 240\,\,\,\left( 2 \right)\)

Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}x + y = 50\\\left( {x + 5} \right)\left( {y + 4} \right) - xy = 240\end{array} \right.\)

Giải hệ phương trình.

Giải hệ phương trình ta được: \[x = 30{\rm{;}}\,y = 20\] (thoả mãn điều kiện).

Vậy chiều dài của vườn ban đầu là \[30m,\] chiều rộng của vườn ban đầu là \[20m.\]