Một tổ công nhân theo kế hoạch phải sản xuất 140 sản phẩm trong thời gian nhất định, mỗi ngày sản xuất số ản phẩm như nhau. Thực tế mỗi ngày sản xuất thêm được 8  sản phẩm so với kế hoạch nên hoàm thành sớm hơn 2 ngày . số sản phẩm phải sản xuất mỗi ngày theo  với kế hoạch của tổ công nhân là

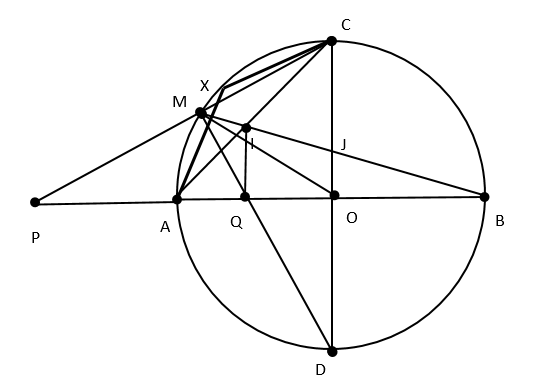
a, do \[AB \bot CD\]tại O nên \[\widehat {POD} = \widehat {BOC} = \widehat {AOC} = {90^0}(1)\]

Xét (O) có \[\widehat {MCD} = {90^0} \Rightarrow DM \bot PC\]TẠI M          \[ \Rightarrow \widehat {PMD} = {90^0}\]

Xét tứ giác OMPD có \[ \Rightarrow \widehat {POD} = \widehat {PMD} = {90^0} \Rightarrow \]TỨ giác OMPD nội tiếp .

b, từ (1) \[ \Rightarrow \] \[\widehat {BOJ} = {90^0}\]

             XÉT (O) có \[\widehat {AMB} = {90^0}\](GOCs nội tiếp chắn nửa đường tròn)

             Xét \[\Delta \]BOJ VÀ  \[\Delta \]BMA có :

              \[\widehat {B{\rm{OJ}}} = \widehat {BMA} = {90^0}\]

               \[\widehat {{\rm{OBJ}}} = \widehat {MBA}\](góc chung)

Do đó \[\Delta B{\rm{OJ}} \sim \Delta BMA\left( {g.g} \right)\] \[ \Rightarrow \frac{{BJ}}{{BO}} = \frac{{BA}}{{BM}} \Rightarrow BJ.BM = BO.BA = R.2R = 2{R^2}\]

c, XÉT (O) có \[\widehat {BMD} = \widehat {BAC}\]( TÍNH CHẤT góc nội tiếp)                                                              \[ \Rightarrow \widehat {IMQ} = \widehat {IAQ}\]

\[ \Rightarrow \]tứ giác AMIQ nội tiếp

\[ \Rightarrow \] \[\widehat {IAQ} + \widehat {AMI} = {180^0} \Rightarrow \widehat {IAQ} + {90^0} = {180^0} \Rightarrow \widehat {IAQ} = {90^0}\]

XÉT \[\Delta AOC\]Có \[\widehat {AOC} = {90^0};OA = OC = R \Rightarrow \Delta AOC\]vuông cân tại O

\[ \Rightarrow \widehat {OAC} = {45^0} \Rightarrow \widehat {IAQ} = {45^0}\]

Xét \[\Delta AQI\]có \[\widehat {AQI} = {90^0};\widehat {IAQ} = {45^0} \Rightarrow \Delta AQI\]vuông cân tại Q

d, tứ giác AOJM nội tiếp nên \[\widehat {MIC} = \widehat {MAQ}\]mà \[\widehat {AMQ} = \widehat {CMB}\](tính chất góc nội tiếp)

do đó \[\Delta MJC \sim \Delta MAQ(g.g) \Rightarrow \frac{{MJ}}{{MC}} = \frac{{MA}}{{MQ}} \Rightarrow MJ.MQ = MA.MC\]

\[{S_{MQJ}} = \frac{1}{2}MJ.MQ.\sin \widehat {MQJ} = \frac{1}{2}MA.MC.\sin {45^0} \le \frac{{\sqrt 2 }}{4}.\frac{{{{\left( {MA + MC} \right)}^2}}}{4}\]

Gọi X là điểm chính giữa của cung nhỏ AC \[ \Rightarrow \]MA+MC\[ \le \]XA+XC(không đổi)

\[{S_{MQJ}} \le \frac{{\sqrt 2 }}{4}.\frac{{{{\left( {XA + XC} \right)}^2}}}{4} = \frac{{{R^2}\left( {\sqrt 2  - 1} \right)}}{2}\](không đổi)

Dấu bằng xảy ra khi \[M \equiv X\]\[ \Rightarrow \]M là điểm chính giữa cung nhỏ AC.

Vậy \[\max {S_{MQJ}} = \frac{{{R^2}\left( {\sqrt 2  - 1} \right)}}{2}\]. Khi M là điểm chính giữa cung nhỏ AC.