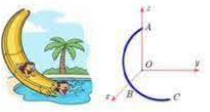
Trong công viên nước, người ta xây dựng một máng trượt nước dạng một cung tròn. Mô hình hóa trong hệ trục \(Oxyz\)(đơn vị trên mỗi trục là \(1\) mét) với điểm đầu máng trượt là \(A\left( {0;0;12} \right)\), cung tròn đi qua điểm \(B\left( {5;12;5} \right)\)và kết thúc ở điểm \(C\left( {17;5;0} \right)\). Tính độ dài máng trượt đó (kết quả cuối cùng làm tròn đến hàng đơn vị)
Câu hỏi trong đề: Đề thi thử Toán Tốt nghiệp THPT 2025-2026 TP. Hồ Chí Minh !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án:
Đáp án: 33
Minh họa lại và mở rộng mô hình như hình vẽ như dưới đây
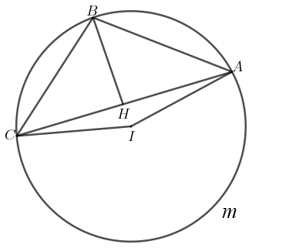
Từ dữ kiện của bài toán ta có: \(\overrightarrow {BA} = \left( { - 5; - 12;7} \right)\); \(\overrightarrow {BC} = \left( {12; - 7; - 5} \right)\); \(\overrightarrow {AC} = \left( {17;5; - 12} \right)\).
Suy ra: \(BA = BC = \sqrt {218} \;;\;AC = \sqrt {458} \). Có \(\Delta ABC\) cân tại \(B\) nên bán kính đường tròn ngoại tiếp của \(\Delta ABC\) là \(R = \frac{{B{C^2}}}{{2AH}} = \frac{{B{C^2}}}{{2\sqrt {B{A^2} - \frac{{A{C^2}}}{4}} }} = \frac{{218}}{{2\sqrt {218 - \frac{{458}}{4}} }} = \frac{{218}}{{3\sqrt {46} }}\).
Mặt khác \(\cos \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right) = \frac{{\overrightarrow {BA} .\overrightarrow {BC} }}{{\left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|}} = \frac{{\left( { - 5} \right).12 + \left( { - 12} \right).\left( { - 7} \right) + 7.\left( { - 5} \right)}}{{\sqrt {{{\left( { - 5} \right)}^2} + {{\left( { - 12} \right)}^2} + {7^2}} .\sqrt {{{12}^2} + {{\left( { - 7} \right)}^2} + {{\left( { - 5} \right)}^2}} }} = - \frac{{11}}{{218}}\).
Hay \(\cos B = - \frac{{11}}{{218}}\). Suy ra \(B \approx 1,6213\;\left( {{\rm{rad}}} \right)\).
Vì cung lớn có số đo \[2B\] nên cung nhỏ có số đo là
\(\alpha = 2\pi - 2B \approx 2\pi - 2 \cdot 1,6213\)\(\left( {{\rm{rad}}} \right)\).
Vậy máng trượt có độ dài là \(l = \alpha R \approx \left( {2\pi - 2 \cdot 1,6213} \right).\frac{{218}}{{3\sqrt {46} }} \approx 32,5772\;\left( {\rm{m}} \right) \approx 33\left( {\rm{m}} \right)\).
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án:
Đáp án: 0,92.
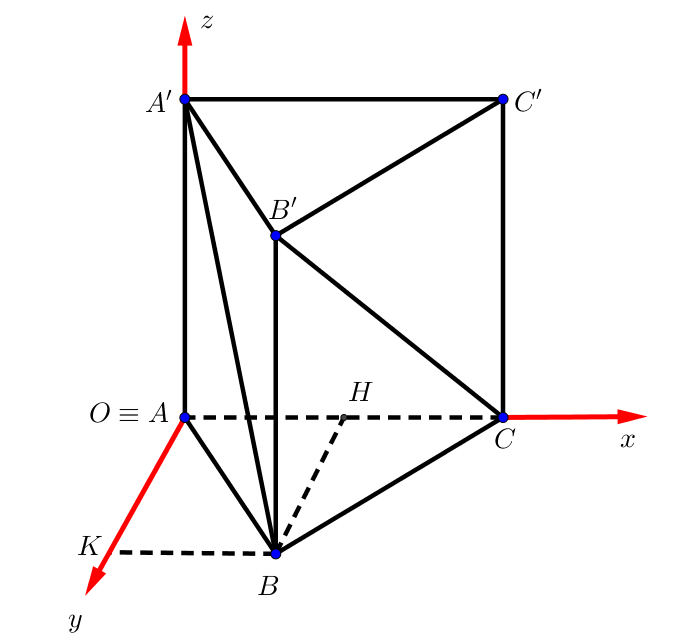
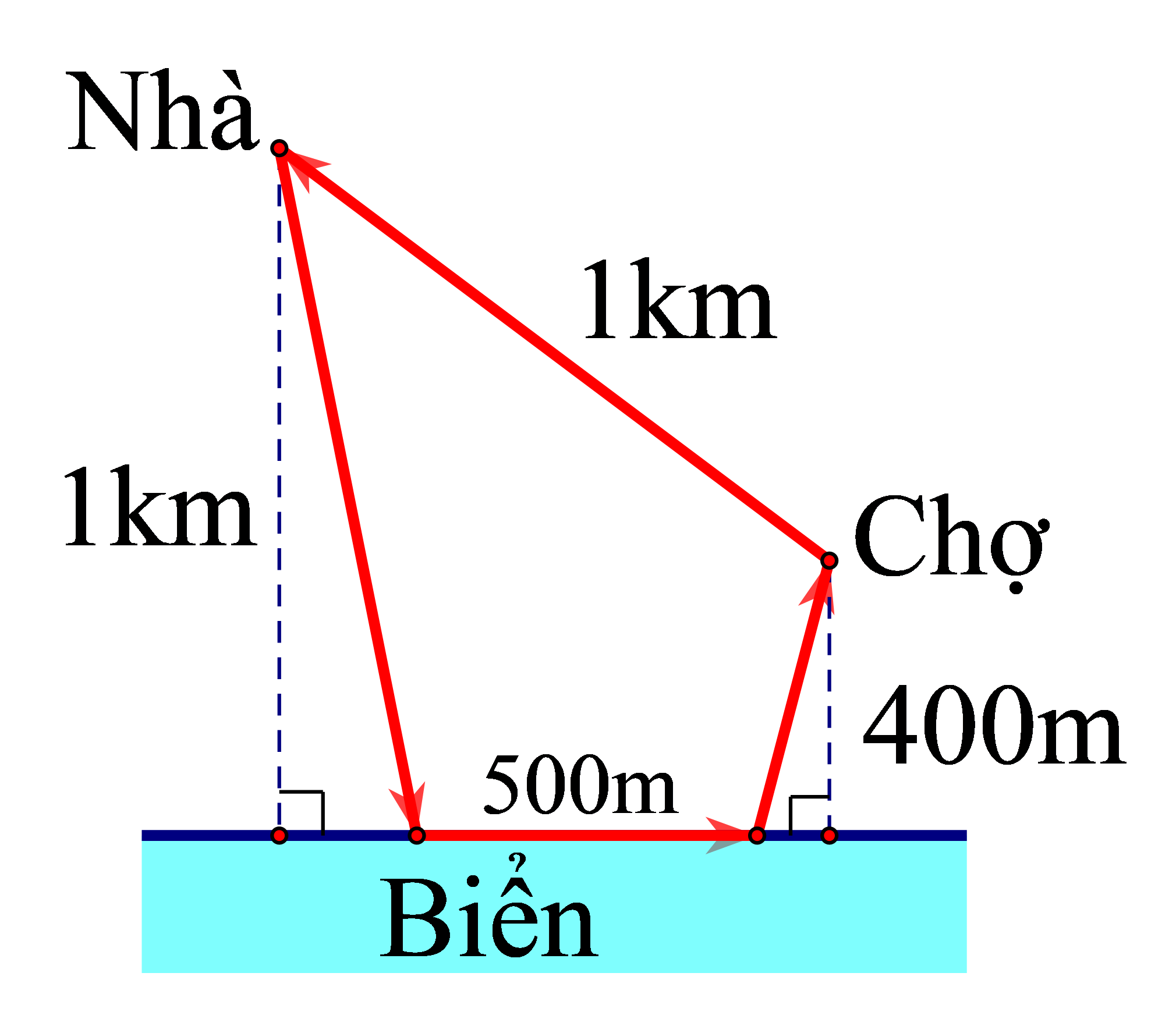
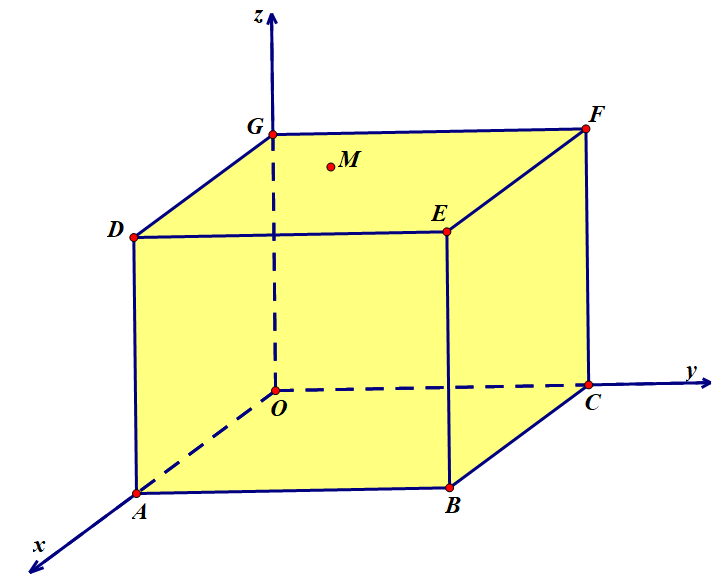
Chọn hệ trục tọa độ \(Oxyz\) như hình vẽ.
Ta tìm được \(A'\left( {0;0;\sqrt 2 } \right)\), \(C\left( {1;0;0} \right)\).
\({x_B} = AH = \frac{1}{2}AC = \frac{1}{2}\).
\({y_B} = BH = \frac{{AC\sqrt 3 }}{2} = \frac{{\sqrt 3 }}{2}\).
Suy ra \(B\left( {\frac{1}{2};\frac{{\sqrt 3 }}{2};0} \right)\).
Do đó \(B'\left( {\frac{1}{2};\frac{{\sqrt 3 }}{2};1} \right)\) (Do \(B\) là hình chiếu của \(B'\) lên \(\left( {Oxy} \right)\)).
\(A'B\) đi qua điểm \(B\left( {\frac{1}{2};\frac{{\sqrt 3 }}{2};0} \right)\) và có 1 vectơ chỉ phương là \(\overrightarrow {A'B} = \left( {\frac{1}{2};\frac{{\sqrt 3 }}{2}; - \sqrt 2 } \right)\).
\(B'C\) đi qua điểm \(C\left( {1;0;0} \right)\) và có 1 vectơ chỉ phương là \(\overrightarrow {B'C} = \left( {\frac{1}{2}; - \frac{{\sqrt 3 }}{2}; - 1} \right)\).
\(d\left( {A'B,B'C} \right) = \frac{{\left| {\left[ {\overrightarrow {A'B} ,\overrightarrow {B'C} } \right] \cdot \overrightarrow {BC} } \right|}}{{\left| {\left[ {\overrightarrow {A'B} ,\overrightarrow {B'C} } \right]} \right|}} \approx 0,92\).
Lời giải
Đáp án:
Đáp án: 7900.
\[C(x) = \int {C'(x)d{\rm{x}} = } \int {(3{{\rm{x}}^2} - 4x + 10} )d{\rm{x}} = {{\rm{x}}^3} - 2{x^2} + 10x + C\]
Ta có \[C(0) = 500 \Rightarrow C = 500 \Rightarrow C(x) = {x^3} - 2{{\rm{x}}^2} + 10{\rm{x}} + 500\]
\[L(x) = 270{\rm{x}} - ({x^3} - 2{{\rm{x}}^2} + 10{\rm{x}} + 500) = - {x^3} + 2{x^2} + 260{\rm{x}} - 500 \Rightarrow L'(x) = - 3{{\rm{x}}^2} + 4{\rm{x}} + 260\].
\[L'(x) = 0 \Leftrightarrow x = 10;x = - \frac{{26}}{3}\]
Vì \[0 \le x \le 20\] nên có \[L(0) = 500;L(10) = 1400;L(20) = 7900\].
Vậy lợi nhuận tối đa là 7900 nghìn đồng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập