Một hộ gia đình sản xuất chiếu cói, mỗi ngày sản xuất được \[x\] chiếc chiếu \[(0 \le x \le 20)\]. Chi phí biên để sản xuất \[x\] chiếc chiếu (nghìn đồng) cho bởi hàm số \[C'(x) = 3{{\rm{x}}^2} - 4x + 10\]( giả sử hàm chi phí là \[C(x)\] thì đạo hàm \[C'(x)\] gọi là chi phí biên, biểu thị tốc độ thay đổi tức thời của chi phí đối với số lượng đơn vị hàng hóa được sản xuất). Biết rằng chi phí cố định ban đầu để sản xuất là 500 nghìn đồng. Giả sử gia đình này bán hết chiếu mỗi ngày với giá 270 nghìn đồng/chiếc chiếu. Tính lợi nhuận tối đa theo đơn vị nghìn đồng mà gia đình đó thu được?

Đáp án: 0,92.

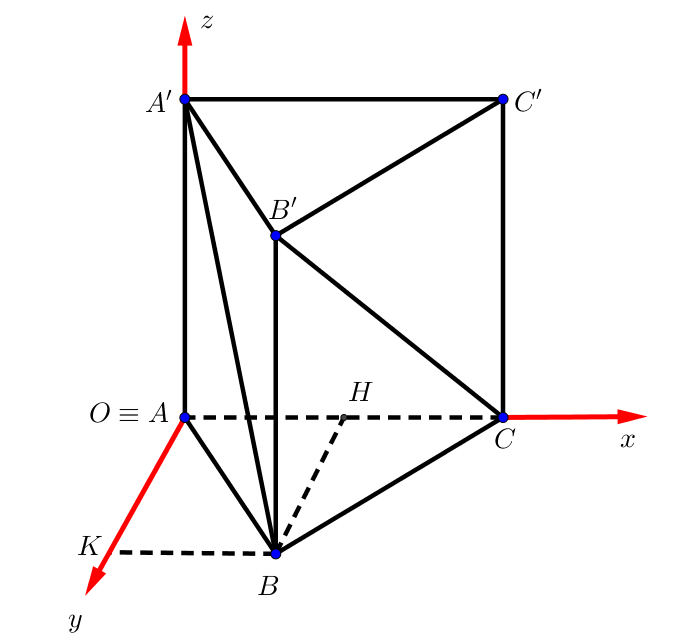
Chọn hệ trục tọa độ \(Oxyz\) như hình vẽ.

Ta tìm được \(A'\left( {0;0;\sqrt 2 } \right)\), \(C\left( {1;0;0} \right)\).

\({x_B} = AH = \frac{1}{2}AC = \frac{1}{2}\).

\({y_B} = BH = \frac{{AC\sqrt 3 }}{2} = \frac{{\sqrt 3 }}{2}\).

Suy ra \(B\left( {\frac{1}{2};\frac{{\sqrt 3 }}{2};0} \right)\).

Do đó \(B'\left( {\frac{1}{2};\frac{{\sqrt 3 }}{2};1} \right)\) (Do \(B\) là hình chiếu của \(B'\) lên \(\left( {Oxy} \right)\)).

\(A'B\) đi qua điểm \(B\left( {\frac{1}{2};\frac{{\sqrt 3 }}{2};0} \right)\) và có 1 vectơ chỉ phương là \(\overrightarrow {A'B}  = \left( {\frac{1}{2};\frac{{\sqrt 3 }}{2}; - \sqrt 2 } \right)\).

\(B'C\) đi qua điểm \(C\left( {1;0;0} \right)\) và có 1 vectơ chỉ phương là \(\overrightarrow {B'C}  = \left( {\frac{1}{2}; - \frac{{\sqrt 3 }}{2}; - 1} \right)\).

\(d\left( {A'B,B'C} \right) = \frac{{\left| {\left[ {\overrightarrow {A'B} ,\overrightarrow {B'C} } \right] \cdot \overrightarrow {BC} } \right|}}{{\left| {\left[ {\overrightarrow {A'B} ,\overrightarrow {B'C} } \right]} \right|}} \approx 0,92\).

Đáp án: 3,92.

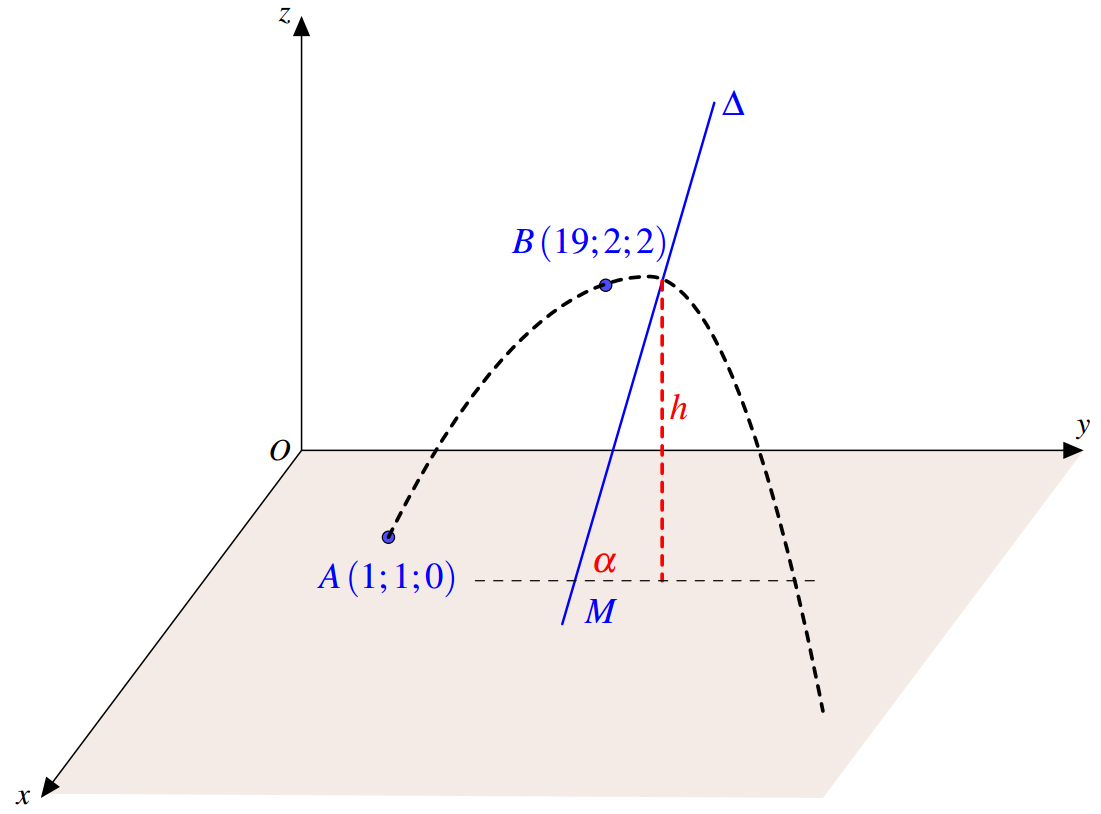
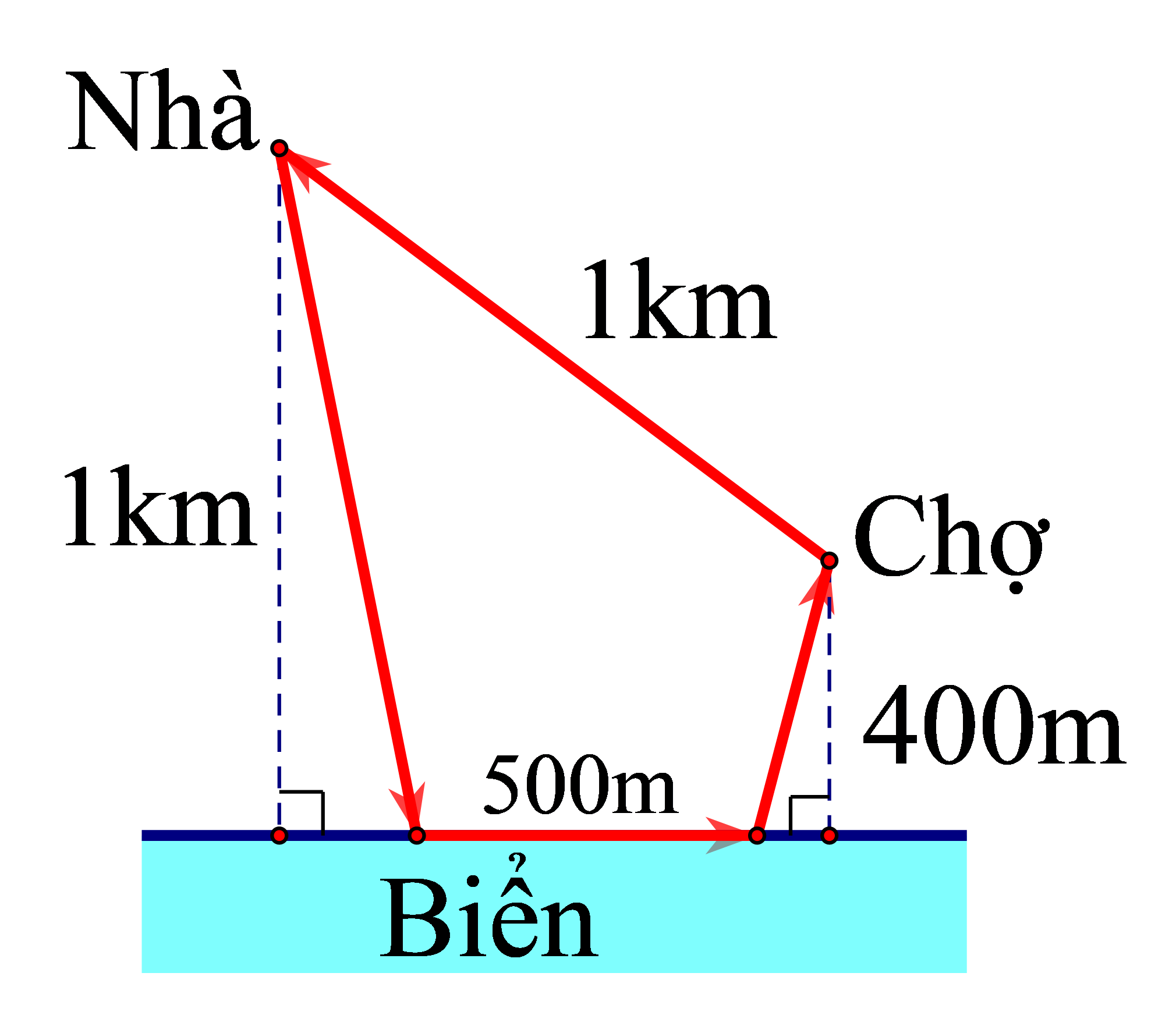
Ta có: \(\overrightarrow {AB}  = \left( {18;1;2} \right) \Rightarrow AB = \sqrt {{{18}^2} + {1^2} + {2^2}}  = \sqrt {329} \).

Gọi \(M = \Delta  \cap \left( {Oxy} \right) \Rightarrow {z_M} = 1 + {t_M} = 0 \Leftrightarrow {t_M} =  - 1 \Rightarrow M\left( {41;31;0} \right)\).

Nên \(\overrightarrow {AM}  = \left( {40;30;0} \right) \Rightarrow AM = \sqrt {{{40}^2} + {{30}^2} + {0^2}}  = 50\).

Gọi  là góc giữa đường thẳng \(\Delta \) và mặt phẳng \(\left( {Oxy} \right)\):

\(\sin \alpha  = \left| {\cos \left( {\overrightarrow {{u_\Delta }} ,\overrightarrow k } \right)} \right| = \frac{{\left| {\overrightarrow {{u_\Delta }} .\overrightarrow k } \right|}}{{\left| {\overrightarrow {{u_\Delta }} } \right|.\left| {\overrightarrow k } \right|}} = \frac{{\left| {3 \times 0 + 4 \times 0 - 1 \times 1} \right|}}{{\sqrt {{3^2} + {{\left( { - 4} \right)}^2} + {1^2}}  \times \sqrt {{0^2} + {0^2} + {1^2}} }} = \frac{{\sqrt {26} }}{{26}}\).

Tích có hướng giữa hai vectơ \[\overrightarrow {AB} \] và \[\overrightarrow {AM} \]:

\[\left[ {\overrightarrow {AB} ,\overrightarrow {AM} } \right] = \left( {\left| {\begin{array}{*{20}{c}}1&2\\{30}&0\end{array}} \right|;\left| {\begin{array}{*{20}{c}}2&{18}\\0&{40}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{18}&1\\{40}&{30}\end{array}} \right|} \right) = \left( { - 60;80;500} \right)\].

Khoảng cách từ điểm \(B\) đến đường thẳng \(AM\):

\[d\left( {B,AM} \right) = \frac{{\left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AM} } \right]} \right|}}{{\left| {\overrightarrow {AM} } \right|}} = \frac{{\sqrt {{{\left( { - 60} \right)}^2} + {{80}^2} + {{500}^2}} }}{{\sqrt {{{40}^2} + {{30}^2} + {0^2}} }} = 2\sqrt {26} \].

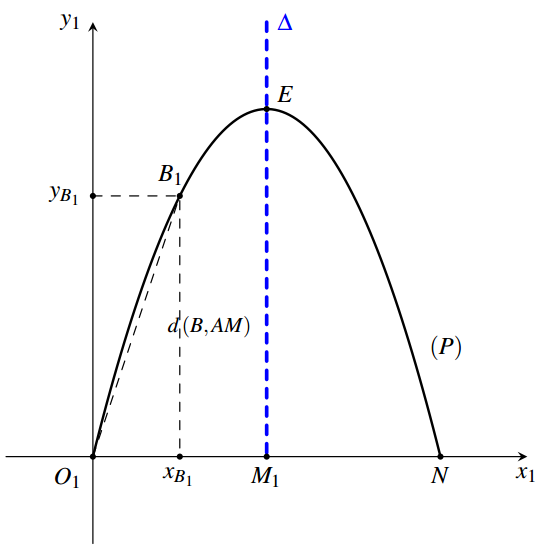
Xét hệ trục mới \[{O_1}{x_1}{y_1}\] với \[{O_1} \equiv A\], \[{O_1}{x_1} \bot \Delta \] và \[{O_1}{y_1}\,{\rm{//}}\,\Delta \].

Parabol \[\left( P \right)\] qua hai điểm \[{O_1}\left( {0;0} \right)\] và \[N\left( {100;0} \right)\]

\[ \Rightarrow \left( P \right):y = ax\left( {x - 100} \right) \Leftrightarrow y = a{x^2} - 100ax\]\[\left( {a \ne 0} \right)\].

Độ cao lớn nhất \(h\) cần tính: \[h = \left| {{y_E}} \right|.\sin \alpha \] với \[E\] là đỉnh của \[\left( P \right)\].

Lại có: \({x_E} = 50 \Rightarrow {y_E} = a \times {50^2} - 100 \times a \times 50 =  - 2500a\).

Trong mặt phẳng \[\left( {{O_1}{x_1}{y_1}} \right)\], điểm \[{B_1}\] tương ứng của điểm \[B\] có tọa độ:

\[\left\{ \begin{array}{l}{y_{{B_1}}} = d\left( {B,AM} \right) = 2\sqrt {26} \\{x_{{B_1}}} = \sqrt {A{B^2} - {d^2}\left( {B,AM} \right)}  = \sqrt {329 - 104}  = 15\end{array} \right. \Rightarrow {B_1}\left( {15;2\sqrt {26} } \right)\].

Điểm \[{B_1} \in \left( P \right) \Rightarrow 2\sqrt {26}  = a \times 225 - 100 \times a \times 15 \Leftrightarrow a =  - \frac{{2\sqrt {26} }}{{1275}}\].

Do đó: \[{y_E} = \left( { - 2500} \right) \times \left( { - \frac{{2\sqrt {26} }}{{1275}}} \right) = \frac{{200\sqrt {26} }}{{51}}\].

Vậy \[h = \frac{{200\sqrt {26} }}{{51}} \times \frac{{\sqrt {26} }}{{26}} = \frac{{200}}{{51}} \approx 3,92\] (mét).